【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.
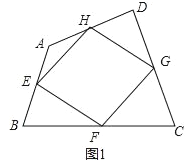
(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
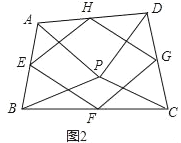
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状,并证明你的猜想.
参考答案:
【答案】(1)见解析;(2)四边形EFGH是菱形;(3)四边形EFGH是正方形.
【解析】分析:(1)如图1中,连接BD,根据三角形中位线定理只要证明EH∥FG,EH=FG即可.
(2)四边形EFGH是菱形.先证明△APC≌△BPD,得到AC=BD,再证明EF=FG即可.
(3)四边形EFGH是正方形,只要证明∠EHG=90°,利用△APC≌△BPD,得∠ACP=∠BDP,即可证明∠COD=∠CPD=90°,再根据平行线的性质即可证明.
详解:(1)如图1,连接BD,
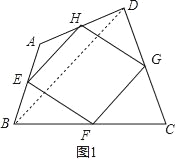
∵点E、H分别为边AB、AD的中点,
∴EH∥BD、EH=![]() BD,
BD,
∵点F、G分别为BC、DC的中点,
∴FG∥BD、FG=![]() BD,
BD,
∴EH=FG、EH∥FG,
∴中点四边形EFGH是平行四边形;
(2)四边形EFGH是菱形,
如图2,连接AC、BD,
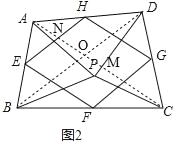
∵∠APB=∠CPD,
∴∠APB+∠APD=∠CPD+∠APD,即∠APC=∠BPD,
在△APC和△BPD中,
AP=BP,∠APC=∠BPD,PC=PD,
∴△APC≌△BPD(SAS),
∴AC=BD,
∵点E、F、G分别为AB、BC、CD的中点,
∴EF=![]() AC、FG=
AC、FG=![]() BD,
BD,
∴EF=FG,
∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形;
(3)四边形EFGH是正方形,
设AC、BD交点为O,AC与PD交于点M,AC与EH交于点N,
∵△APC≌△BPD,
∴∠ACP=∠BDP,
∵∠DMO=∠CMP,
∴∠COD=∠CPD=90°,
∵EH∥BD、AC∥HG,
∴∠EHG=∠ENO=∠BOC=∠DOC=90°,
∵四边形EFGH是菱形,
∴四边形EFGH是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OE平分∠AOD,OF⊥OC,
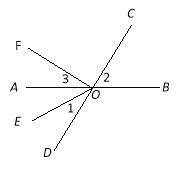
(1)图中∠AOF的余角是 (把符合条件的角都填出来);
(2)如果∠AOC=160°,那么根据 可得∠BOD= 度;
(3)如果∠1=32°,求∠2和∠3的度数.
-
科目: 来源: 题型:
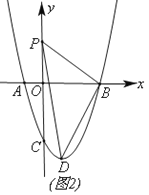
查看答案和解析>>【题目】如图,在平面直角坐标中,抛物线y=ax2-2ax-3a(a≠0)与x轴交于A、B(A在B的左侧),与y轴交于点C,且OC=3OA.
(1)如图(1)求抛物线的解析式;
(2)如图(2)动点P从点O出发,沿y轴正方向以每秒1个单位的速度移动,点D是抛物线顶点,连接PB、PD、BD,设点P运动时间为t(单位:秒),△PBD的面积为S,求S与t的函数关系式;
(3)如图(3)在(2)的条件下,延长BP交抛物线于点Q,过点O作OE⊥BQ,垂足为E,连接CE、CB,若CE=CB,求t值,并求出此时的Q点坐标.


-
科目: 来源: 题型:
查看答案和解析>>【题目】用双十字相乘法分解因式
例:20x2+9xy-18y2-18x+33y-14。

∵4×6+5×(-3)=9,4×(-7)+5×2=-13,-3×(-7)+2×6=33,
∴20x2+9xy-18y2-18x+33y-14=(4x-3y+2)(5x+6y-7)。
双十字相乘法的理论根据是多项式的乘法,在使用双十字相乘法时,应注意它带有试验性质,很可能需要经过多次试验才能得到正确答案。
分解因式6x2-5xy-6y2-2xz-23yz-20z2=
-
科目: 来源: 题型:
查看答案和解析>>【题目】某食品厂从生产的袋装食品中抽出样品20袋,检测每袋的重量是否符合标准,超过或不足的部分分别用正、负数来表示,记录如下表:
与标准重量的差值(单位:g)
﹣5
﹣2
0
1
3
6
袋数
1
4
3
4
5
3
(1)计算这批样品的平均重量,判断它比标准重量重还是轻多少?
(2)若标准重量为450克,则这批样品的总重量是多少?
(3)若这种食品的合格标准为450±5克,则这批样品的合格率为 (直接填写答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
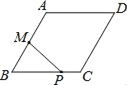
A.
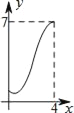 B.
B. 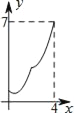 C.
C. 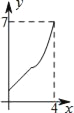 D.
D. 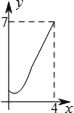
-
科目: 来源: 题型:
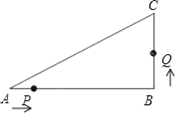
查看答案和解析>>【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P开始从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm,点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.
(1)出发2秒后,求PQ的长;
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,则求出几秒后第一次形成等腰三角形;若不能,则说明理由;
相关试题

