【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”。图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速,设运动的时间为t秒,问:
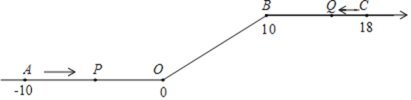
(1)动点P从点A运动至点C需要________秒;
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少?
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
参考答案:
【答案】(1)19秒;(2)相遇点M所对应的数是![]() ;(3)t的值为2、6.5、11或17
;(3)t的值为2、6.5、11或17
【解析】
(1)根据路程除以速度等于时间,可得答案;
(2)根据相遇时P,Q运动的时间相等,可得方程,解方程,可得答案;
(3)根据PO与BQ相等,可得方程,解方程,可得答案.
解:(1)点P运动至点C时,所需时间t=![]() (秒);
(秒);
(2)由题可知,P、Q两点相遇在线段OB上于M处,设OM=![]() .
.
则![]() ,
,
解得![]() ,故相遇点M所对应的数是
,故相遇点M所对应的数是![]() ;
;
(3)P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等有4种可能:
①动点Q在CB上,动点P在AO上,则:8-t=10-2t,解得:t=2.
②动点Q在CB上,动点P在OB上,则:8-t=(t-5)×1,解得:t=6.5.
③动点Q在BO上,动点P在OB上,则:2(t-8)=(t-5)×1,解得:t=11.
④动点Q在OA上,动点P在BC上,则:10+2(t-15)=t-13+10,解得:t=17.
综上所述:t的值为2、6.5、11或17.
-
科目: 来源: 题型:
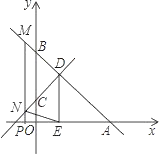
查看答案和解析>>【题目】直线y=﹣x+6与x轴交于A,与y轴交于B,直线CD与y轴交于C(0,2)与直线AB交于D,过D作DE⊥x轴于E(2,0).
(1)求直线CD的函数解析式;
(2)P是x轴上一动点,过P作x轴的垂线,分别与直线AB,CD交于M,N,设MN的长为d,P点的横坐标为t,求出d与t之间的函数关系式;
(3)在(2)的条件下,当t为何值时,以M,N,E,D为顶点的四边形是平行四边形.(直接写出结果)
-
科目: 来源: 题型:
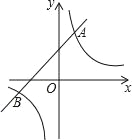
查看答案和解析>>【题目】如图,一次函数y1=kx+b(k≠0)与反比例函数y2=
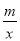 (m≠0)相交于A和B两点.且A点坐标为(1,3),B点的横坐标为﹣3.
(m≠0)相交于A和B两点.且A点坐标为(1,3),B点的横坐标为﹣3.(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出使得y1≤y2时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为4厘米,E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E,向终点E以每秒a厘米的速度运动,设运动时间为t秒,△PBF的面积记为S. S与t的部分函数图象如图2所示,已知点M(1,
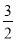 )、N(5,6)在S与t的函数图象上.
)、N(5,6)在S与t的函数图象上.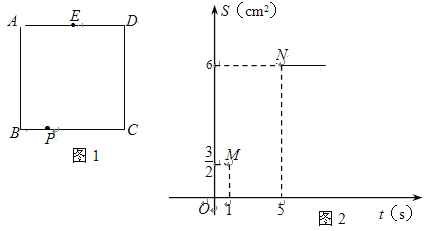
(1)求线段BF的长及a的值;
(2)写出S与t的函数关系式,并补全该函数图象;
(3)当t为多少时,△PBF的面积S为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O中,点A为弧BC中点,BD为直径,过A作AP∥BC交DB的延长线于点P.
(1)求证:PA是⊙O的切线;
(2)若BC=2
 ,AB=2
,AB=2 ,求sin∠ABD的值.
,求sin∠ABD的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:﹣32÷(﹣3)2+3×(﹣2)+|﹣4|
(2)计算:
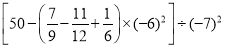
(3)化简:(5a2+2a﹣1)﹣4[3﹣2(4a+a2)]
(4)化简:3x2﹣[7x﹣(4x﹣3)﹣2x2]
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2
 的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ;连接PQ,PQ与BC交于点E,QP延长线与AD(或AD延长线)交于点F,连接CQ.求证:
的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ;连接PQ,PQ与BC交于点E,QP延长线与AD(或AD延长线)交于点F,连接CQ.求证:(1)CQ=AP;
(2)△APB∽△CEP.

相关试题

