【题目】如图1,正方形ABCD的边长为4厘米,E为AD边的中点,F为AB边上一点,动点P从点B出发,沿B→C→D→E,向终点E以每秒a厘米的速度运动,设运动时间为t秒,△PBF的面积记为S. S与t的部分函数图象如图2所示,已知点M(1,![]() )、N(5,6)在S与t的函数图象上.
)、N(5,6)在S与t的函数图象上.
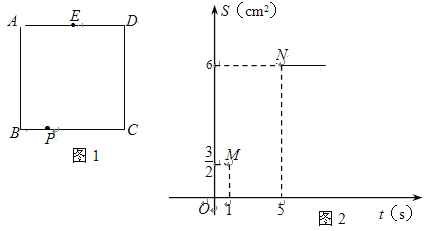
(1)求线段BF的长及a的值;
(2)写出S与t的函数关系式,并补全该函数图象;
(3)当t为多少时,△PBF的面积S为4.
参考答案:
【答案】(1)BF=3,a=1;(2)当0≤t≤4时,S=![]() t;当4<t≤8时,S=6;当8<t≤10时,S=18-
t;当4<t≤8时,S=6;当8<t≤10时,S=18-![]() t.图像见解析;(3)t=
t.图像见解析;(3)t=![]() 或
或![]() .
.
【解析】
试题分析:(1)根据图2可以看出,当t=5时,P在CD上,此时△PBF的高就为正方形的边长,底为BF,利用面积等于6,可求得BF,再根据t=1时,△PBF的面积为![]() ,可求得a的值;(2)由点P运动过程,可发现△PBF的面积有3种情况,分别是:当0≤t≤4时,此时P在AB上,当4<t≤8时,此时P在CD上,当8<t≤10时,此时P在AD上,分别求出解析式即可.再根据解析式可补全图像;(3)把S=4分别代入解析式中即可求出t值.
,可求得a的值;(2)由点P运动过程,可发现△PBF的面积有3种情况,分别是:当0≤t≤4时,此时P在AB上,当4<t≤8时,此时P在CD上,当8<t≤10时,此时P在AD上,分别求出解析式即可.再根据解析式可补全图像;(3)把S=4分别代入解析式中即可求出t值.
试题解析:(1)由题意可知,当t=5时,S△PBF=![]() ×4BF=6,BF=3.当t=1时,S△PBF=
×4BF=6,BF=3.当t=1时,S△PBF=![]() at×3=
at×3=![]() ,a=1;(2)当0≤t≤4时,设S=kt,把(1,
,a=1;(2)当0≤t≤4时,设S=kt,把(1,![]() )代入得,k=
)代入得,k=![]() ,S=
,S=![]() t;当4<t≤8时,S=6;当8<t≤10时,设S=mt+b,把(8,6),(10,3)代入,得
t;当4<t≤8时,S=6;当8<t≤10时,设S=mt+b,把(8,6),(10,3)代入,得![]() ,解得
,解得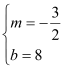 ,S=18-
,S=18-![]() t.综上所述,当0≤t≤4时,S=
t.综上所述,当0≤t≤4时,S=![]() t;当4<t≤8时,S=6;当8<t≤10时,S=18-
t;当4<t≤8时,S=6;当8<t≤10时,S=18-![]() t,据此可补全图像,如下图:
t,据此可补全图像,如下图:
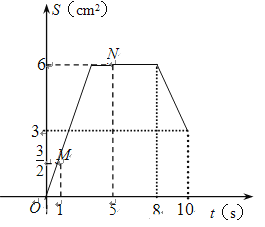
(3)当S=4时,![]() t=4,t=
t=4,t=![]() ;18-
;18-![]() t=4,t=
t=4,t=![]() .∴当t=
.∴当t=![]() 或 t=
或 t=![]() 时△PBF的面积S为4.
时△PBF的面积S为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若m﹣n=2,m+n=5,则m2+n2的值为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1﹣a,5)与点B(3,b)关于y轴对称,则a﹣b的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一个粒子在第一象限和x,y轴的正半轴上运动,在第一秒内,它从原点运动到(0,1),接着它按图所示在x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒运动一个单位长度,那么2010秒时,这个粒子所处位置为( )
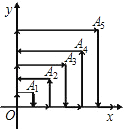
A.(14,44) B.(15,44) C.(44,14) D.(44,15)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在平面直角坐标系xOy中,反比例函数y1=
 (x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
(x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).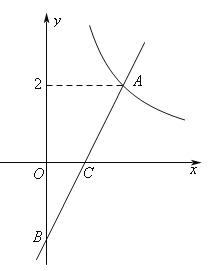
(1)求一次函数的解析式;
(2)观察图像,直接写出使y1≥y2的x的取值范围.
(3)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,请写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. 4a2﹣4a2=4a B. (﹣a3b)2=a6b2 C. a+a=a2 D. a24a4=4a8
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的两边长为3和8,第三边长为奇数,则第三边长为( )
A. 5或7 B. 7或9 C. 7 D. 9
相关试题

