【题目】如图,点A、B的坐标分别为(4,0)、(0,8),点C是线段OB上一动点,点E在x轴正半轴上,四边形OEDC是矩形,且OE=2OC.设OE=t(t>0),矩形OEDC与△AOB重合部分的面积为S.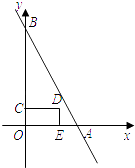
根据上述条件,回答下列问题:
(1)当矩形OEDC的顶点D在直线AB上时,求t的值;
(2)当t=4时,求S的值;
(3)直接写出S与t的函数关系式(不必写出解题过程);
(4)若S=12,则t= .
参考答案:
【答案】
(1)
解:由题意可得∠BCD=∠BOA=90°,∠CBD=∠OBA,
∴△BCD∽△BOA,
∴ ![]()
而 ![]() ,
,
则 ![]() ,
,
解得 ![]() ,
,
∴当点D在直线AB上时, ![]() .
.
(2)
解:当t=4时,点E与A重合,设CD与AB交于点F,
则由△CBF∽△OBA得 ![]() ,
,
即 ![]() ,
,
解得CF=3,
∴ ![]() .
.
(3)
解:①当 ![]() 时,
时, ![]()
②当 ![]() 时,
时, ![]()
③当4<t≤16时, ![]()
分析:①当 ![]() 时,如图(1),
时,如图(1),
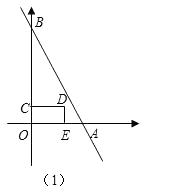
②当 ![]() 时,如图(2),
时,如图(2),
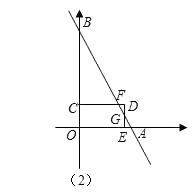
∵A(4,0),B(0,8),∴直线AB的解析式为y=﹣2x+8,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() =
= ![]()
③当4<t≤16时,如图(3)
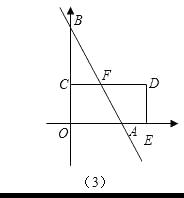
∵CD∥OA,∴△BCF∽△BOA,∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]()
(4)8
【解析】分析:由题意可知把S=12代入 ![]() 中,
中, ![]() ,
,
整理,得t2﹣32t+192=0,
解得t1=8,t2=24>16(舍去),
∴当S=12时,t=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生对“垃圾分类”知识的了解程度,某学校对本校学生进行抽样调查,并绘制统计图,其中统计图中没有标注相应人数的百分比.请根据统计图回答下列问题:
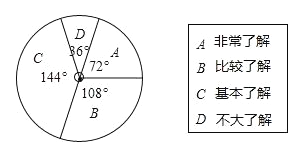
(1)求“非常了解”的人数的百分比.
(2)已知该校共有1200名学生,请估计对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE.
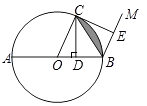
(1)当∠COB=60°时,直接写出阴影部分的面积;
(2)求证:CE是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了迎接“6.1儿童节“,以调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
第1个
第2个
第3个
第4个
…
第n个
调整前单价x (元)
x1
x2=6
x3=72
x4
…
xn
调整后单价y (元)
y1
y2=4
y3=59
y4
…
yn
当这些玩具调整后的单价都大于2元时,解答下列问题:
(1)y与x的函数关系式为,x的取值范围为;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了元;
(3)这n个玩具调整前、后的平均单价分别为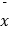 (元)、
(元)、  (元),猜想
(元),猜想  与
与 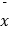 的关系式,并写出推导过程.
的关系式,并写出推导过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题情景:
如图,在直角坐标系xOy中,点A、B为二次函数y=ax2(a>0)图象上的两点,且点A、B的横坐标分别为m、n(m>n>0),连接OA、AB、OB.设△AOB的面积为S时,解答下列问题: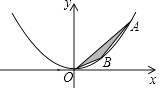
(1)探究:当a=1时,mn
m﹣n
S
m=3,n=1
3
2
m=5,n=2
10
3
当a=2时,
2mn
m﹣n
S
m=3,n=1
6
2
m=5,n=2
20
3
(2)归纳证明:对任意m、n(m>n>0),猜想S=(用a,m,n表示),并证明你的猜想.
(3)拓展应用:
若点A、B的横坐标分别为m、n(m>0>n),其它条件不变时,△AOB的面积S=(用a,m,n表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九年级学生共450人,其中男生250人,女生200人.该校对九年级所有学生进行了一次体育测试,并随机抽取了50名男生和40名女生的测试成绩作为样本进行分析,绘制成如下的统计表:
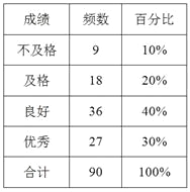
(1)请解释“随机抽取了50名男生和40名女生”的合理性;
(2)从上表的“频数”、“百分比”两列数据中选择一列,用适当的统计图表示;
(3)估计该校九年级学生体育测试成绩不及格的人数.
-
科目: 来源: 题型:
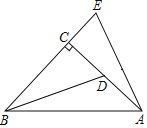
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且CE=CD,试猜想BD和AE的关系,并说明你猜想的正确性.
相关试题

