搜索
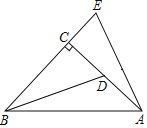
【题目】如图，已知Rt△ABC中，∠ACB=90°，CA=CB，D是AC上一点，E在BC的延长线上，且CE=CD，试猜想BD和AE的关系，并说明你猜想的正确性．
参考答案：
【答案】猜想：BD=AE ，BD⊥AE．
【解析】
猜想：BD=AE ，BD⊥AE，先证明△BDC≌△AEC得出BD=AE，∠CBD=∠CAE，从而得出∠BFE=90°，即BF⊥AE．
解：猜想：BD=AE ，BD⊥AE．
理由：延长BD交AE于点F，
∵∠ACB=90°，
∴∠ACE=∠BCD=90°．
又BC=AC，CD=CE，
∴△BDC≌△AEC（HL）．
∴BD=AE
∴∠CBD=∠CAE．
又∠CAE+∠E=90°．
∴∠EBF+∠E=90°．
∴∠BFE=90°，∴BF⊥AE，即BD⊥AE．
-
科目： 来源： 题型：
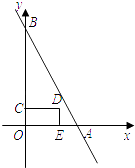
查看答案和解析>>【题目】如图，点A、B的坐标分别为（4，0）、（0，8），点C是线段OB上一动点，点E在x轴正半轴上，四边形OEDC是矩形，且OE=2OC．设OE=t（t＞0），矩形OEDC与△AOB重合部分的面积为S．
根据上述条件，回答下列问题：
（1）当矩形OEDC的顶点D在直线AB上时，求t的值；
（2）当t=4时，求S的值；
（3）直接写出S与t的函数关系式（不必写出解题过程）；
（4）若S=12，则t= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】问题情景：
如图，在直角坐标系xOy中，点A、B为二次函数y=ax2（a＞0）图象上的两点，且点A、B的横坐标分别为m、n（m＞n＞0），连接OA、AB、OB．设△AOB的面积为S时，解答下列问题：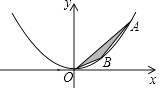
（1）探究：当a=1时，mn
m﹣n
S
m=3，n=1
3
2
m=5，n=2
10
3
当a=2时，
2mn
m﹣n
S
m=3，n=1
6
2
m=5，n=2
20
3
（2）归纳证明：对任意m、n（m＞n＞0），猜想S=（用a，m，n表示），并证明你的猜想．
（3）拓展应用：
若点A、B的横坐标分别为m、n（m＞0＞n），其它条件不变时，△AOB的面积S=（用a，m，n表示）． -
科目： 来源： 题型：
查看答案和解析>>【题目】某中学九年级学生共450人，其中男生250人，女生200人．该校对九年级所有学生进行了一次体育测试，并随机抽取了50名男生和40名女生的测试成绩作为样本进行分析，绘制成如下的统计表：
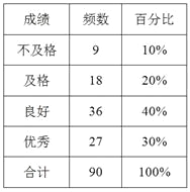
(1)请解释“随机抽取了50名男生和40名女生”的合理性；
(2)从上表的“频数”、“百分比”两列数据中选择一列，用适当的统计图表示；
(3)估计该校九年级学生体育测试成绩不及格的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某社区从2011年开始，组织全民健身活动，结合社区条件，开展了广场舞、太极拳、羽毛球和跑步四个活动项目，现将参加项目活动总人数进行统计，并绘制成每年参加总人数折线统计图和2015年各活动项目参与人数的扇形统计图，请你根据统计图解答下列题
（1）2015年比2011年增加 人；
（2）请根据扇形统计图求出2015年参与跑步项目的人数；
（3）组织者预计2016年参与人员人数将比2015年的人数增加15%，名各活动项目参与人数的百分比与2016年相同，请根据以上统计结果，估计2016年参加太极拳的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，…，按此规律排列，则第⑩个图形中小圆圈的个数为( )
A. 24 B. 27 C. 30 D. 33
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义:若
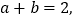则称
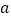与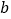
是关于1的平衡数。(1)5与______是关于1的平衡数；
(2)
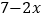与________是关于1的平衡数(用含
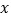的代数式表示)；(3)若
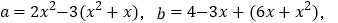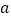判断与是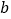否是关于1的平衡数,并说明理由。
相关试题
