搜索
【题目】为了解学生对“垃圾分类”知识的了解程度，某学校对本校学生进行抽样调查，并绘制统计图，其中统计图中没有标注相应人数的百分比．请根据统计图回答下列问题：
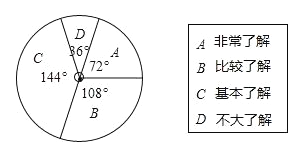
（1）求“非常了解”的人数的百分比．
（2）已知该校共有1200名学生，请估计对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人？
参考答案：
【答案】（1）20%；（2）600
【解析】
试题分析：（1）根据扇形统计图可以求得“非常了解”的人数的百分比；（2）根据扇形统计图可以求得对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人．
试题解析：（1）由题意可得，
“非常了解”的人数的百分比为：
， 即“非常了解”的人数的百分比为20%；
（2）由题意可得，
对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有：1200×
=600（人），
即对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有600人
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解本校七年级700名学生上学期参加社会实践活动的时间，随机对该年级50名学生进行了调查．根据收集的数据绘制了频数分布直方图，则以下说法正确的是( )
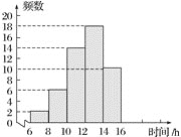
A. 学生参加社会实践活动时间最多的是16 h
B. 学生参加社会实践活动的时间大多数是12～14 h
C. 学生参加社会实践活动时间不少于10 h的为84%
D. 由样本可以估计全年级700人中参加社会实践活动时间为6～8 h的大约有26人
-
科目： 来源： 题型：
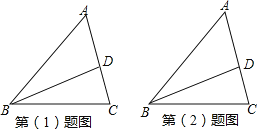
查看答案和解析>>【题目】如图，已知BD为△ABC的角平分线请按如下要求操作与解答：
（1）过点D画DE∥BC交AB于点E．若∠A=68°，∠AED=42°，求△BCD各内角的度数；
（2）画△ABC的角平分线CF交BD于点M，若∠A=60°，请找出图中所有与∠A相等的角，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】服装厂为了估计某校七年级学生穿每种尺码校服的人数，从该校七年级学生中随机抽取了50名学生的身高数据(单位：cm)，绘制成了下面的频数分布表和频数分布直方图.
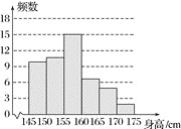
(1)表中m＝________，n＝________；
(2)身高x满足160≤x＜170的校服记为L号，则需要订购L号校服的学生占被调查学生的百分数为________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O的直径AB=4，C是⊙O上一点，连接OC．过点C作CD⊥AB，垂足为D，过点B作BM∥OC，在射线BM上取点E，使BE=BD，连接CE．
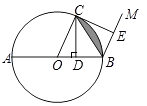
（1）当∠COB=60°时，直接写出阴影部分的面积；
（2）求证：CE是⊙O的切线． -
科目： 来源： 题型：
查看答案和解析>>【题目】某商场为了迎接“6.1儿童节“，以调低价格的方式促销n个不同的玩具，调整后的单价y（元）与调整前的单价x（元）满足一次函数关系，如表：
第1个
第2个
第3个
第4个
…
第n个
调整前单价x （元）
x1
x2=6
x3=72
x4
…
xn
调整后单价y （元）
y1
y2=4
y3=59
y4
…
yn
当这些玩具调整后的单价都大于2元时，解答下列问题：
（1）y与x的函数关系式为，x的取值范围为；
（2）某个玩具调整前单价是108元，顾客购买这个玩具省了元；
（3）这n个玩具调整前、后的平均单价分别为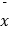
（元）、 
（元），猜想 与 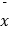的关系式，并写出推导过程． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A、B的坐标分别为（4，0）、（0，8），点C是线段OB上一动点，点E在x轴正半轴上，四边形OEDC是矩形，且OE=2OC．设OE=t（t＞0），矩形OEDC与△AOB重合部分的面积为S．
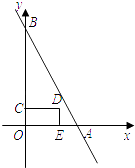
根据上述条件，回答下列问题：
（1）当矩形OEDC的顶点D在直线AB上时，求t的值；
（2）当t=4时，求S的值；
（3）直接写出S与t的函数关系式（不必写出解题过程）；
（4）若S=12，则t= ．
相关试题
