【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.得平行四边形ABDC
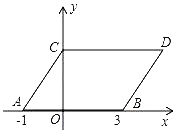
(1)直接写出点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC , 求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
请画出图形,直接写出∠CPO、∠DCP、∠BOP的数量关系.
参考答案:
【答案】(1)C(0,2),D(4,2)(2)(0,4)或(0,﹣4)(3)①当点P在BD上,∠CPO=∠DCP+∠BOP,②当点P在线段BD的延长线上时,∠CPO=∠BOP﹣∠DCP,③当点P在线段DB的延长线上时,∠CPO=∠DCP﹣∠BOP
【解析】分析:(1)、根据点的平移法则得出点C和点D的坐标;(2)、设M坐标为(0,m),然后求出平行四边形的性质的面积,根据面积相等得出m的值,从而得出点M的坐标;(3)、分当点P在BD上、当点P在线段BD的延长线上时和当点P在线段DB的延长线上时三种情况分别画出图形,然后得出答案.
详解:(1)、∵将A(﹣1,0),B(3,0)分别向上平移2个单位,再向右平移1个单位,
∴C(0,2),D(4,2);
(2)、∵AB=4,CO=2, ∴S平行四边形ABDC=ABCO=4×2=8, 设M坐标为(0,m),
∴ ![]() ×4×|m|=8,解得m=±4, ∴M点的坐标为(0,4)或(0,﹣4);
×4×|m|=8,解得m=±4, ∴M点的坐标为(0,4)或(0,﹣4);
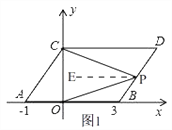
(3)、①当点P在BD上,如图1, 由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD, ∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠CPE+∠OPE=∠DCP+∠BOP,
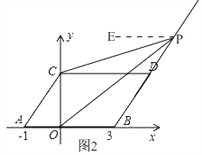
②当点P在线段BD的延长线上时,如图2, 由平移的性质得,AB∥CD,
过点P作PE∥AB,则PE∥CD, ∴∠DCP=∠CPE,∠BOP=∠OPE,
∴∠CPO=∠OPE﹣∠CPE=∠BOP﹣∠DCP,
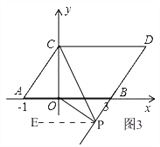
③当点P在线段DB的延长线上时,如图3, 同(2)的方法得出∠CPO=∠DCP﹣∠BOP.
-
科目: 来源: 题型:
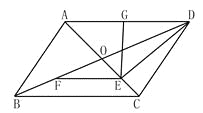
查看答案和解析>>【题目】如图,在平行四边形ABCD中,BD=2AB,AC与BD相交于点O,点E、F、G分别是OC、OB、AD的中点.
求证:(1)DE⊥OC;
(2)EG=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明将他的7次数学测验成绩按顺序绘成了两幅统计图,依此来观察自己近期数学的学习情况和成绩的进步情况.
(1)甲、乙两幅统计图所表示的数据相同吗?甲图和乙图给人造成的感觉各是什么?
(2)若小明要向他的父母说明他的数学成绩在努力后的情况,他将向父母展示哪幅统计图,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.求:
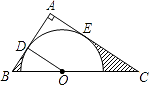
(1)tanC;
(2)图中两部分阴影面积的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
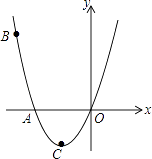
(1)求抛物线的函数解析式;
(2)连接BC交x轴于点F.试在y轴负半轴上找一点P,使得△POC∽△BOF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块分别均匀的等腰三角形蛋糕(AB=AC且AB≠BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
这条分割直线既平分了三角形的面积,又平分了三角形的周长,我们称这条直线为三角形的“等分积周线”.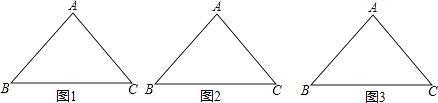
(1)小明很快就想到了一条经过点A分割直线,请你用尺规作图在图1中画出这条“等分积周线(不写画法).
(2)小华觉得小明的方法很好,所以自己模仿着在图2中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?请说明理由.
(3)若AB=BC=5,BC=6,请你通过计算,在图3中找出△ABC不经过顶点的一条“等分积周线”. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A、B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金 (元/辆)
400
280
红星中学根据实际情况,计划租用A、B型客车共5辆,同时送八年级师生到基地参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题.
(1)若要保证租车费用不超过1900元,求x的最大值;
(2)在(1)的条件下,若八年级师生共有195人,请设计一种最省钱的租车方案.
相关试题

