【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.求: 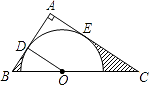
(1)tanC;
(2)图中两部分阴影面积的和.
参考答案:
【答案】
(1)解:连接OE,
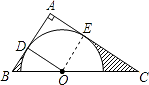
∵AB、AC分别切⊙O于D、E两点,
∴AD⊥OD,AE⊥OE,
∴∠ADO=∠AEO=90°,
又∵∠A=90°,
∴四边形ADOE是矩形,
∵OD=OE,
∴四边形ADOE是正方形,
∴OD∥AC,OD=AD=3,
∴∠BOD=∠C,
∴在Rt△BOD中, ![]() ,
,
∴ ![]() .
.
答:tanC= ![]()
(2)解:如图,设⊙O与BC交于M、N两点,
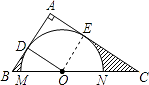
由(1)得:四边形ADOE是正方形,
∴∠DOE=90°,
∴∠COE+∠BOD=90°,
∵在Rt△EOC中, ![]() =
= ![]() ,OE=3,
,OE=3,
∴ ![]() ,
,
∴S扇形DOM+S扇形EON=S扇形DOE= ![]() ,
,
∴S阴影=S△BOD+S△COE﹣(S扇形DOM+S扇形EON)= ![]() ,
,
答:图中两部分阴影面积的和为 ![]() .
.
【解析】(1)连接OE,得到∠ADO=∠AEO=90°,根据∠A=90°,推出矩形ADOE,进一步推出正方形ADOE,得出OD∥AC,OD=AD=3,∠BOD=∠C,即可求出答案;(2)设⊙O与BC交于M、N两点,由(1)得:四边形ADOE是正方形,推出∠COE+∠BOD=90°,根据 ![]() ,OE=3,求出
,OE=3,求出 ![]() ,根据S扇形DOM+S扇形EON=S扇形DOE , 即可求出阴影部分的面积.
,根据S扇形DOM+S扇形EON=S扇形DOE , 即可求出阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究性学习小组,为了解本校七年级学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分),对本校的七年级学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图如图所示,请结合统计图中提供的信息,回答下列问题.
(1)这个研究性学习小组所抽取的学生有多少人?
(2)在被调查的学生中,一天做家庭作业所用的大致时间超过120分(不包括120分)的人数占被调查学生总人数的百分之几?

-
科目: 来源: 题型:
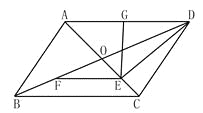
查看答案和解析>>【题目】如图,在平行四边形ABCD中,BD=2AB,AC与BD相交于点O,点E、F、G分别是OC、OB、AD的中点.
求证:(1)DE⊥OC;
(2)EG=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明将他的7次数学测验成绩按顺序绘成了两幅统计图,依此来观察自己近期数学的学习情况和成绩的进步情况.
(1)甲、乙两幅统计图所表示的数据相同吗?甲图和乙图给人造成的感觉各是什么?
(2)若小明要向他的父母说明他的数学成绩在努力后的情况,他将向父母展示哪幅统计图,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.得平行四边形ABDC
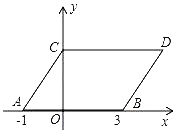
(1)直接写出点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC , 求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
请画出图形,直接写出∠CPO、∠DCP、∠BOP的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
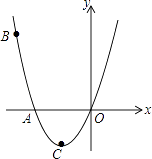
(1)求抛物线的函数解析式;
(2)连接BC交x轴于点F.试在y轴负半轴上找一点P,使得△POC∽△BOF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块分别均匀的等腰三角形蛋糕(AB=AC且AB≠BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
这条分割直线既平分了三角形的面积,又平分了三角形的周长,我们称这条直线为三角形的“等分积周线”.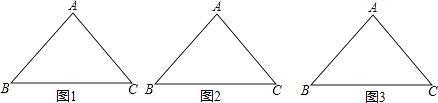
(1)小明很快就想到了一条经过点A分割直线,请你用尺规作图在图1中画出这条“等分积周线(不写画法).
(2)小华觉得小明的方法很好,所以自己模仿着在图2中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?请说明理由.
(3)若AB=BC=5,BC=6,请你通过计算,在图3中找出△ABC不经过顶点的一条“等分积周线”.
相关试题

