【题目】如图,已知抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C. 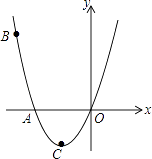
(1)求抛物线的函数解析式;
(2)连接BC交x轴于点F.试在y轴负半轴上找一点P,使得△POC∽△BOF.
参考答案:
【答案】
(1)解:设抛物线的解析式为y=ax2+bx+c (a≠0),
将点A(﹣2,0)、B(﹣3,3)、0(0,0),
代入可得: 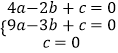
解得:a=1,b=2,c=0,
所以抛物线的解析式为y=x2+2x
(2)解:如图,
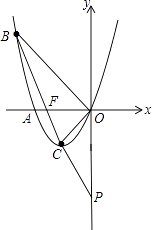
∵y=x2+2x=(x+1)2﹣1,
∴顶点C的坐标为(﹣1,﹣1).
∵B(﹣3,3),
∴tan∠BOF= ![]() =1,tan∠POC=
=1,tan∠POC= ![]() =1,
=1,
∴∠BOF=45°,∠POC=45°.
∴∠POC=∠BOF,
∴∠POC=45°=∠BOF,
设直线BC的解析式为y=kx+b(k≠0),
∵直线经过点B(﹣3,3)、C(﹣1,﹣1),
∴ ![]()
解得:k=﹣2,b=﹣3,
∴直线BC解析式为y=﹣2x﹣3,
令y=0,得x=﹣ ![]() ,
,
因此,点F(﹣ ![]() ,0),
,0),
∴OF= ![]() ,OB=
,OB= ![]() =3
=3 ![]() ,
,
OC= ![]() =
= ![]() ,
,
∵∠POC=∠BOF,
∴当 ![]() =
= ![]() 时,△POC∽△BOF,
时,△POC∽△BOF,
代入求出OP=4,
即当P点的坐标为(0,﹣4)时,△POC∽△BOF.
【解析】(1)抛物线的解析式为y=ax2+bx+c (a≠0),把A、B、C的坐标代入求出即可;(2)求出∠BOF=∠POC,求出OB、OF、OC的长,根据相似得出比例式,代入求出即可.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明将他的7次数学测验成绩按顺序绘成了两幅统计图,依此来观察自己近期数学的学习情况和成绩的进步情况.
(1)甲、乙两幅统计图所表示的数据相同吗?甲图和乙图给人造成的感觉各是什么?
(2)若小明要向他的父母说明他的数学成绩在努力后的情况,他将向父母展示哪幅统计图,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.求:
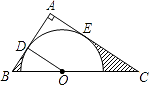
(1)tanC;
(2)图中两部分阴影面积的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.得平行四边形ABDC
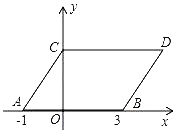
(1)直接写出点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC , 求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
请画出图形,直接写出∠CPO、∠DCP、∠BOP的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块分别均匀的等腰三角形蛋糕(AB=AC且AB≠BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
这条分割直线既平分了三角形的面积,又平分了三角形的周长,我们称这条直线为三角形的“等分积周线”.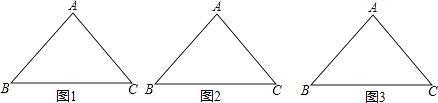
(1)小明很快就想到了一条经过点A分割直线,请你用尺规作图在图1中画出这条“等分积周线(不写画法).
(2)小华觉得小明的方法很好,所以自己模仿着在图2中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?请说明理由.
(3)若AB=BC=5,BC=6,请你通过计算,在图3中找出△ABC不经过顶点的一条“等分积周线”. -
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A、B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金 (元/辆)
400
280
红星中学根据实际情况,计划租用A、B型客车共5辆,同时送八年级师生到基地参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题.
(1)若要保证租车费用不超过1900元,求x的最大值;
(2)在(1)的条件下,若八年级师生共有195人,请设计一种最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕顶点C逆时针旋转得到△A′B′C′,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( )
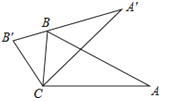
A.30°
B.35°
C.40°
D.45°
相关试题

