【题目】某公交公司有A、B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金 (元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A、B型客车共5辆,同时送八年级师生到基地参加社会实践活动.设租用A型客车x辆,根据要求回答下列问题.
(1)若要保证租车费用不超过1900元,求x的最大值;
(2)在(1)的条件下,若八年级师生共有195人,请设计一种最省钱的租车方案.
参考答案:
【答案】(1)x的最大值为4;(2)最省钱的方案是A型3辆,B型2辆
【解析】分析:(1)根据题意,表示出租车总费用,列出不等式即可解决;
(2)由(1)得出x的取值范围,一一列举计算,排除不合题意方案即可.
详解:(1)∵载客量=汽车辆数×单车载客量,租金=汽车辆数×单车租金,
∴B型客车载客量=30(5x);B型客车租金=280(5x);
根据题意,![]() ,解得:
,解得:![]()
∴x的最大值为4;
(1)由(1)可知, ![]() 故x可能取值为0、1、2、3、4,
故x可能取值为0、1、2、3、4,
①A型0辆,B型5辆,租车费用为400×0+280×5=1400元,但载客量为45×0+30×5=150<195,故不合题意舍去;
②A型1辆,B型4辆,租车费用为400×1+280×4=1520元,但载客量为45×1+30×4=165<195,故不合题意舍去;
③A型2辆,B型3辆,租车费用为400×2+280×3=1640元,但载客量为45×2+30×3=180<195,故不合题意舍去;
④A型3辆,B型2辆,租车费用为400×3+280×2=1760元,但载客量为45×3+30×2=195=195,符合题意;
⑤A型4辆,B型1辆,租车费用为400×4+280×1=1880元,但载客量为45×4+30×1=210,符合题意;
故符合题意的方案有④⑤两种,最省钱的方案是A型3辆,B型2辆。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.得平行四边形ABDC
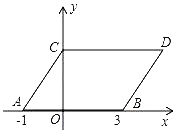
(1)直接写出点C,D的坐标;
(2)若在y轴上存在点 M,连接MA,MB,使S△MAB=S平行四边形ABDC , 求出点M的坐标.
(3)若点P在直线BD上运动,连接PC,PO.
请画出图形,直接写出∠CPO、∠DCP、∠BOP的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过点A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
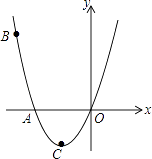
(1)求抛物线的函数解析式;
(2)连接BC交x轴于点F.试在y轴负半轴上找一点P,使得△POC∽△BOF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一块分别均匀的等腰三角形蛋糕(AB=AC且AB≠BC),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
这条分割直线既平分了三角形的面积,又平分了三角形的周长,我们称这条直线为三角形的“等分积周线”.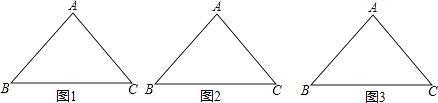
(1)小明很快就想到了一条经过点A分割直线,请你用尺规作图在图1中画出这条“等分积周线(不写画法).
(2)小华觉得小明的方法很好,所以自己模仿着在图2中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?请说明理由.
(3)若AB=BC=5,BC=6,请你通过计算,在图3中找出△ABC不经过顶点的一条“等分积周线”. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕顶点C逆时针旋转得到△A′B′C′,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( )
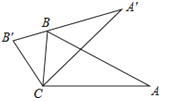
A.30°
B.35°
C.40°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的三个顶点都在格点上.
(1)将
 ABC绕着点B顺时针旋转
ABC绕着点B顺时针旋转 ,得到
,得到 A1B1C1.
A1B1C1.(2)画出
 ABC关于原点的对称图形
ABC关于原点的对称图形 A2B2C2
A2B2C2(3)若点P(a,b)是
 ABC边上的任意一点,则P关于原点对称的点Q坐标为_______.(用含a,b的式子表示)
ABC边上的任意一点,则P关于原点对称的点Q坐标为_______.(用含a,b的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(﹣3,7)
B.(﹣1,7)
C.(﹣4,10)
D.(0,10)
相关试题

