【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为边作△CDE,其中CD=CE,∠DCE=90°,连接BE.

(1)求证:△ACD≌△BCE.
(2)若AB=6cm,则BE=______cm.
(3)BE与AD有何位置关系?请说明理由.
参考答案:
【答案】(1)证明见解析;(2)12;(3)垂直平分.
【解析】
(1)根据等腰直角三角形的性质得到CD=CE,CA=CB,然后利用“SAS”可判断△ACD≌△BCE即可;
(2)根据全等三角形的性质得到AD=BE即可;
(3)由全等三角形的性质得出∠EBC=∠A,由△ABC是等腰直角三角形,则∠A=∠ABC=∠EBC=45°,则BE⊥AD,即可得到答案.
解:(1)证明:∵△CDE是等腰直角三角形,∠DCE=90°,
∴CD=CE,
∵∠ACB=90°,
∴∠ACB=∠DCE,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中, ,
,
∴△ACD≌△BCE(SAS);
(2)解:∵DB=AB,
∴AD=2AB=12cm,
由(1)得:△ACD≌△BCE,
∴BE=AD=12cm;
故答案为:12;
(3)由△ACD≌△BCE,
∴∠EBC=∠A,
∵△ABC是等腰直角三角形,
∴∠A=∠ABC=∠EBC=45°,
∴∠ABE=90°,
即BE⊥AD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知长方形ABCD中,∠A=∠D=∠B=∠C=90,E是AD上的一点,F是AB上的一点,EF⊥EC,且EF=EC,DE=4cm.

(1)求证:AF=DE.
(2)若AD+DC=18,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某造纸企业为了更好地处理污水问题,决定购买10台新型污水处理设备.甲、乙两种型号的设备可选,其中每台的价格,月处理污水量如表:
A型
B型
价格(万元/)
10
8
处理污水量(吨/月)
180
150
(1)经预算:该企业购买污水处理设备的资金不超过85万元,你认为该企业有哪几种购买方案.
(2)在(1)的条件下,若每月需要处理的污水不低于1530吨,为了节约资金,请你为该企业设计一种最省钱的购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图①
图②
图③
三个角上三个数的积
1×(﹣1)×2=﹣2
(﹣3)×(﹣4)×(﹣5)=﹣60
三个角上三个数的和
1+(﹣1)+2=2
(﹣3)+(﹣4)+(﹣5)=﹣12
积与和的商
(﹣2)÷2=﹣1
(2)请用你发现的规律求出图④中的数x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,一次函数y=kx+b的图象与反比例函数y=
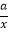 的图象交A(1,4),B(-4,c)两点,
的图象交A(1,4),B(-4,c)两点,如图2所示,点M、N都在直线AB上,过M、N分别作y轴的平行线交双曲线于E、F,设M、N的横坐标分别为m、n,且 4 < m < 0 , n > 1 ,请探究,当m、n满足什么关系时,ME=NE.
(1)求反比例函数及一次函数的解析式;
(2)点P是x轴上一动点,使|PA-PB|的值最大,求点P的坐标及△PAB的面积;
(3)如图2所示,点M、N都在直线AB上,过M、N分别作y轴的平行线交双曲线于E、F,设M、N的横坐标分别为m、n,且
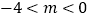 , n>1,请探究,当m、n满足什么关系时,ME=NE.
, n>1,请探究,当m、n满足什么关系时,ME=NE. 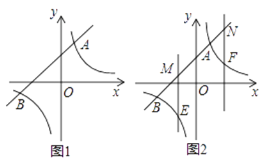
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是按规律排列的一列式子:
第1个式子:
 ;
;第2个式子:
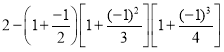 ;
;第3个式子:
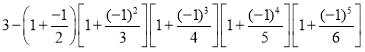 ;
;……
(1)分别计算出这三个式子的结果;
(2)请按规律写出第2019个式子的形式(中间部分用省略号,两端部分必须写详细);
(3)计算第2019个式子的结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 在某次数学测试中,满分为100分,各测试内容及所占分值的分布情况如下扇形统计图,则以下结论正确的是( )
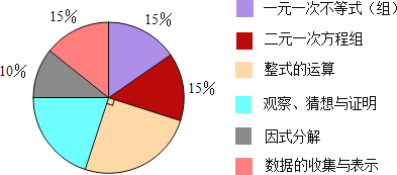
①一元一次不等式(组)部分与二元一次方程组部分所占分值一样
②因式分解部分在试卷上占10分
③整式的运算部分在整张试卷中所占比例为25%
④观察、猜想与证明部分的圆心角度数为72°
A.①②③B.②③④C.①④D.①②③④
相关试题

