【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:△NDE≌△MAE;
(2)求证:四边形AMDN是平行四边形;
(3)当AM的值为何值时,四边形AMDN是矩形?请说明理由.

参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)当AM=1时,四边形AMDN为矩形,理由见解析.
【解析】
(1)由菱形的性质可知ND∥AM,可证得∠DNE=∠AME,结合E为AD的中点,可利用AAS证得结论;
(2)由(1)可得ND=AM,根据一组对边平行且相等的四边形是平行四边形可证得结论;
(3)若四边形AMDN是矩形,则可求得AM=![]() AD,则可求得答案.
AD,则可求得答案.
(1)证明:
∵四边形ABCD为菱形,
∴CD∥AB,
∴∠DNE=∠AME,
∵E为AD的中点,
∴DE=AE,
在△NDE和△MAE中
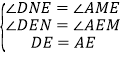
∴△NDE≌△MAE(AAS);
(2)证明:
由(1)可知△NDE≌△MAE,
∴ND=AM,且ND∥AM,
∴四边形AMDN为平行四边形;
(3)解:当AM=1时,四边形AMDN为矩形,
理由如下:
若四边形AMDN为矩形,则∠AMD=90°,
∵∠DAM=60°,
∴∠ADM=30°,
∴AM=![]() AD=
AD=![]() AB=1,
AB=1,
故当AM=1时,四边形AMDN为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)请用两种不同的方法求图②中阴影部分的面积:
方法1: 方法2:
(2)观察图②请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系. ;
(3)根据(2)题中的等量关系,解决:已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知
 于点D,AE平分
于点D,AE平分
(1)试探究
 与
与 的关系;
的关系; (2)若F是AE上一动点,当F移动到AE之间的位置时,
 ,如图2所示,此时
,如图2所示,此时 的关系如何?
的关系如何?(3)若F是AE上一动点,当F继续移动到AE的延长线上时,如图3,
 ,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.
,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.
-
科目: 来源: 题型:
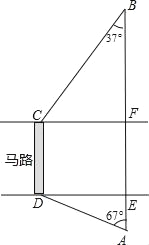
查看答案和解析>>【题目】如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市,CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.求CD与AB之间的距离.(参考数据:sin67°≈
 ,cos67°≈
,cos67°≈ ,tan67°≈
,tan67°≈ ,sn37°≈
,sn37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题7分)如图,一次函数
 的图象与x轴交于点B,与反比例函数
的图象与x轴交于点B,与反比例函数 的图象的一个交点为A(2,m).
的图象的一个交点为A(2,m).
(1)求反比例函数的表达式;
(2)求当x满足什么范围时,
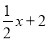 <
< ;
;(3)过点A作AC⊥x轴,垂足为点C,如果求点P在反比例函数图象上,且△PBC的面积等于6,请直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为以AQ为腰的等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)在AC段的抛物线上有一点R到直线AC的距离最大,请直接写出点R的坐标.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF.其中正确的有( )

A.1个B.2个C.3个D.4个
相关试题

