【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)请用两种不同的方法求图②中阴影部分的面积:
方法1: 方法2:
(2)观察图②请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系. ;
(3)根据(2)题中的等量关系,解决:已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;

参考答案:
【答案】(1)(m-n)2;(m+n)2-4mn;(2)(m-n)2=(m+n)2-4mn;(3)1.
【解析】
(1)方法1:表示出阴影部分的边长,然后利用正方形的面积公式列式;
方法2:利用大正方形的面积减去四周四个矩形的面积列式;
(2)根据不同方法表示的阴影部分的面积相同解答;
(3)根据(2)的结论整体代入进行计算即可得解.
解:(1)方法1:∵阴影部分的四条边长都是m-n,是正方形,
∴阴影部分的面积=(m-n)2
方法2:∵阴影部分的面积=大正方形的面积减去四周四个矩形的面积
∴阴影部分的面积=(m+n)2-4mn;
(2)根据(1)中两种计算阴影部分的面积方法可知(m-n)2=(m+n)2-4mn;
(3)由(2)可知(a+b)2=(a-b)2+4ab,
∵a-b=5,ab=-6,
∴(a+b)2=(a-b)2+4ab=52+4×(-6)=25-24=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点,若∠A=60°,则∠BMN的度数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中正确的序号是_____.
①△ABE的面积等于△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图。

(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知
 于点D,AE平分
于点D,AE平分
(1)试探究
 与
与 的关系;
的关系; (2)若F是AE上一动点,当F移动到AE之间的位置时,
 ,如图2所示,此时
,如图2所示,此时 的关系如何?
的关系如何?(3)若F是AE上一动点,当F继续移动到AE的延长线上时,如图3,
 ,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.
,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.
-
科目: 来源: 题型:
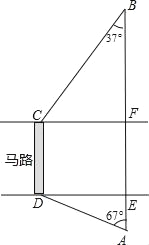
查看答案和解析>>【题目】如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市,CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.求CD与AB之间的距离.(参考数据:sin67°≈
 ,cos67°≈
,cos67°≈ ,tan67°≈
,tan67°≈ ,sn37°≈
,sn37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:△NDE≌△MAE;
(2)求证:四边形AMDN是平行四边形;
(3)当AM的值为何值时,四边形AMDN是矩形?请说明理由.

相关试题

