【题目】(本小题7分)如图,一次函数![]() 的图象与x轴交于点B,与反比例函数
的图象与x轴交于点B,与反比例函数![]() 的图象的一个交点为A(2,m).
的图象的一个交点为A(2,m).

(1)求反比例函数的表达式;
(2)求当x满足什么范围时,![]() <
<![]() ;
;
(3)过点A作AC⊥x轴,垂足为点C,如果求点P在反比例函数图象上,且△PBC的面积等于6,请直接写出点P的坐标.
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() ; (3) (3,2)(-3,-2)
; (3) (3,2)(-3,-2)
【解析】
试题(1)先将点A(2,m)代入反比例函数![]() 求得A的坐标,然后代入
求得A的坐标,然后代入![]() ,求得k的值(2)首先求出两函数交点的坐标,再结合反比例函数和一次函数的图像即可求出:
,求得k的值(2)首先求出两函数交点的坐标,再结合反比例函数和一次函数的图像即可求出:![]() 的解集.
的解集.
(3) 可求得点B的坐标,设P(x,y),由![]() ,即可求得x,y的值.
,即可求得x,y的值.
试题解析:
解;(1)∵一次函数![]() 的图象经过点A,
的图象经过点A,
∴m=3,
∴点A的坐标为(2,3),
∵反比例函数![]() 的图象经过点A(2,3),
的图象经过点A(2,3),
∴k=6,
∴反比例函数的表达式:![]() .
.
(2)联立反比例函数和一次函数的解析式:
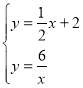
解得:![]() 或
或![]() ,
,
∴![]() 的解集为x<-6或0﹤x﹤2;
的解集为x<-6或0﹤x﹤2;
(3)令![]() ,解得:x=-4,即B(-4,0),
,解得:x=-4,即B(-4,0),
∵AC⊥x轴
∴C(2,0),
∴BC=6,
设P(x,y),
∵![]()
∴![]() 或
或![]() ,
,
分别代入![]() 中,
中,
得![]() 或
或![]()
∴P(3,2)或P(-3,-2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知
 于点D,AE平分
于点D,AE平分
(1)试探究
 与
与 的关系;
的关系; (2)若F是AE上一动点,当F移动到AE之间的位置时,
 ,如图2所示,此时
,如图2所示,此时 的关系如何?
的关系如何?(3)若F是AE上一动点,当F继续移动到AE的延长线上时,如图3,
 ,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.
,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.
-
科目: 来源: 题型:
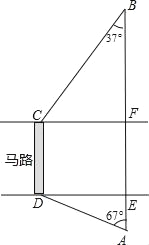
查看答案和解析>>【题目】如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市,CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.求CD与AB之间的距离.(参考数据:sin67°≈
 ,cos67°≈
,cos67°≈ ,tan67°≈
,tan67°≈ ,sn37°≈
,sn37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:△NDE≌△MAE;
(2)求证:四边形AMDN是平行四边形;
(3)当AM的值为何值时,四边形AMDN是矩形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=
 x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.(1)求该二次函数的解析式及点C的坐标;
(2)当点P运动到B点时,点Q停止运动,这时,在x轴上是否存在点E,使得以A,E,Q为顶点的三角形为以AQ为腰的等腰三角形?若存在,请求出E点坐标;若不存在,请说明理由.
(3)在AC段的抛物线上有一点R到直线AC的距离最大,请直接写出点R的坐标.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法①△BDF≌△CDE;②△ABD和△ACD面积相等;③BF∥CE;④CE=BF.其中正确的有( )

A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距480km,一辆货车从甲地匀速驶往乙地,货车出发一段时间后,一辆汽车从乙地匀速驶往甲地,设货车行驶的时间为
 线段OA表示货车离甲地的距离
线段OA表示货车离甲地的距离 与xh的函数图象;折线BCDE表示汽车距离甲地的距离
与xh的函数图象;折线BCDE表示汽车距离甲地的距离 与
与 的函数图象.
的函数图象. 求线段OA与线段CD所表示的函数表达式;
求线段OA与线段CD所表示的函数表达式; 若OA与CD相交于点F,求点F的坐标,并解释点F的实际意义;
若OA与CD相交于点F,求点F的坐标,并解释点F的实际意义; 当x为何值时,两车相距100千米?
当x为何值时,两车相距100千米?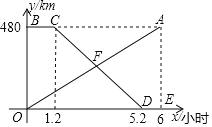
相关试题

