【题目】如图,在△ABC中,已知![]() 于点D,AE平分
于点D,AE平分![]()
(1)试探究![]() 与
与![]() 的关系;
的关系;
(2)若F是AE上一动点,当F移动到AE之间的位置时,![]() ,如图2所示,此时
,如图2所示,此时![]() 的关系如何?
的关系如何?
(3)若F是AE上一动点,当F继续移动到AE的延长线上时,如图3,![]() ,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.
,①中的结论是否还成立?如果成立请说明理由,如果不成立,写出新的结论.

参考答案:
【答案】(1)∠EAD=![]() (∠C-∠B),理由见解析;
(∠C-∠B),理由见解析;
(2)∠EFD=![]() (∠C-∠B),理由见解析;
(∠C-∠B),理由见解析;
(3)∠AFD=![]() (∠C-∠B)成立,理由见解析.
(∠C-∠B)成立,理由见解析.
【解析】
(1)由图不难发现∠EAD=∠EAC-∠DAC,再根据三角形的内角和定理结合角平分线的定义分别用结论中出现的角替换∠EAC和∠DAC;
(2)作![]() 于G转化为(1)中的情况,利用(1)的结论即可解决;
于G转化为(1)中的情况,利用(1)的结论即可解决;
(3)作![]() 于H转化为(1)中的情况,利用(1)的结论即可解决.
于H转化为(1)中的情况,利用(1)的结论即可解决.
解:(1)∠EAD=![]() (∠C-∠B).理由如下:
(∠C-∠B).理由如下:
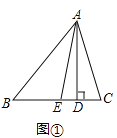
∵AE平分∠BAC,
∴∠BAE=∠CAE=![]() ∠BAC
∠BAC
∵∠BAC=180°-(∠B+∠C)
∴∠EAC=![]() [180°-(∠B+∠C)]
[180°-(∠B+∠C)]
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=90°-∠C,
∵∠EAD=∠EAC-∠DAC
∴∠EAD=![]() [180°-(∠B+∠C)]-(90°-∠C)=
[180°-(∠B+∠C)]-(90°-∠C)=![]() (∠C-∠B).
(∠C-∠B).
(2)∠EFD=![]() (∠C-∠B).理由如下:
(∠C-∠B).理由如下: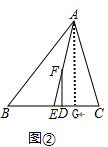
作![]() 于G
于G
由(1)可知∠EAG=![]() (∠C-∠B)
(∠C-∠B)
∵![]() ,
,![]()
∴FD∥AG
∴∠EAG=∠EFD
∴∠EFD=![]() (∠C-∠B)
(∠C-∠B)
(3)∠AFD=(∠C-∠B).理由如下:
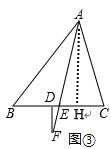
作![]() 于H
于H
由(1)可知∠EAH=![]() (∠C-∠B)
(∠C-∠B)
∵![]() ,
,![]()
∴FD∥AH
∴∠EAH=∠AFD
∴∠AFD=![]() (∠C-∠B)
(∠C-∠B)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中正确的序号是_____.
①△ABE的面积等于△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图。

(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐。据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐?
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.(1)请用两种不同的方法求图②中阴影部分的面积:
方法1: 方法2:
(2)观察图②请你写出下列三个代数式:(m+n)2,(m﹣n)2,mn之间的等量关系. ;
(3)根据(2)题中的等量关系,解决:已知:a﹣b=5,ab=﹣6,求:(a+b)2的值;

-
科目: 来源: 题型:
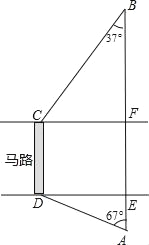
查看答案和解析>>【题目】如图,马路的两边CF、DE互相平行,线段CD为人行横道,马路两侧的A、B两点分别表示车站和超市,CD与AB所在直线互相平行,且都与马路的两边垂直.马路宽20米,A,B相距62米,∠A=67°,∠B=37°.求CD与AB之间的距离.(参考数据:sin67°≈
 ,cos67°≈
,cos67°≈ ,tan67°≈
,tan67°≈ ,sn37°≈
,sn37°≈ ,cos37°≈
,cos37°≈ ,tan37°≈
,tan37°≈ )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.
(1)求证:△NDE≌△MAE;
(2)求证:四边形AMDN是平行四边形;
(3)当AM的值为何值时,四边形AMDN是矩形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题7分)如图,一次函数
 的图象与x轴交于点B,与反比例函数
的图象与x轴交于点B,与反比例函数 的图象的一个交点为A(2,m).
的图象的一个交点为A(2,m).
(1)求反比例函数的表达式;
(2)求当x满足什么范围时,
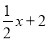 <
< ;
;(3)过点A作AC⊥x轴,垂足为点C,如果求点P在反比例函数图象上,且△PBC的面积等于6,请直接写出点P的坐标.
相关试题

