搜索
【题目】如图， 在△ABC中，E是BC边上一点，沿AE折叠，点B恰好落在AC边上的点D处，若∠BAC=60°，BE=CD，则∠AED=______ 度.
参考答案：
【答案】70
【解析】由折叠的性质可知，DE=BE，∠ADE=∠ABE，∠DAE=∠BAE=
∠BAC=30°，
∵BE=CD，
∴DE=DC，
∴∠C=∠DEC，
∴∠ADE=∠C+∠DEC=2∠C.
∴∠ABC=2∠C，
又∵∠BAC=60°，∠BAC+∠ABC+∠C=180°，
∴∠ABC+∠C=180°-60°=120°，即3∠C=120°，解得：∠C=40°，
∴∠ADE=40°×2=80°，
∴∠AED=180°-∠DAE-∠ADE=180°-30°-80°=70°.
故答案为：70.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知CD是经过∠BCA顶点C的一条直线，CA=CB．E、F分别是直线CD上两点，且∠BEC=∠CFA=∠
．
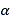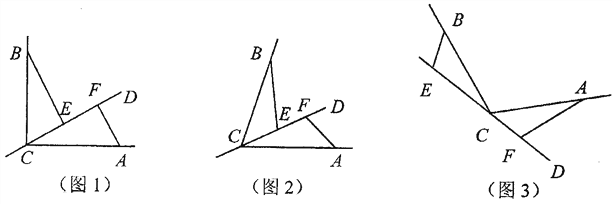
(1)若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面问题：
①如图1若∠BCA=90°，∠
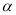=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.②如图2，若0°＜∠BCA＜180°， 请添加一个关于∠
与∠BCA关系的条件___ ____使①中的结论仍然成立；(2)如图3，若直线CD经过∠BCA的外部，∠
=∠BCA，请写出三条线段EF、BE、AF的数量关系并证明你的结论. -
科目： 来源： 题型：
查看答案和解析>>【题目】在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的，∠BAC=90°，AB=6，AC=8，点D，E，F，G，H，I都在长方形KLMJ的边上，则长方形KLMJ的面积为（
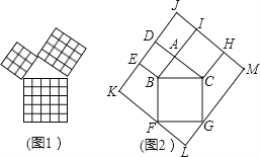
A. 360 B. 400 C. 440 D. 484
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A在函数
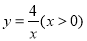图像上，过点A作x轴和y轴的平行线分别交函数
图像于点B、C，直线BC与坐标轴的交点为D、E．当点A在函数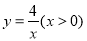
图像上运动时，
（1）设点A横坐标为a，则点B的坐标为 ，点C的坐标为 （用含a的字母表示）；
（2）△ABC的面积是否发生变化？若不变，求出△ABC的面积，若变化，请说明理由；
（3）请直接写出BD与CE满足的数量关系．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB、CD相交于点O，∠BOM=90°，∠DON=90°．
（1）若∠COM=∠AOC，求∠AOD的度数；
（2）若∠COM=
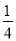∠BOC，求∠AOC和∠MOD．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在扇形AOB中，OA、OB是半径，且OA＝4，∠AOB＝120°．点P是弧AB上的一个动点，连接AP、BP，分别作OC⊥PA，OD⊥PB，垂足分别为C、D，连接CD．
（1）如图①，在点P的移动过程中，线段CD的长是否会发生变化？若不发生变化，请求出线段CD的长；若会发生变化，请说明理由；
（2）如图②，若点M、N为
的三等分点，点I为△DOC的外心．当点P从点M运动到N点时，点I所经过的路径长为__________．（直接写出结果）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线l1∥l2，且l3和l1，l2分别交于A，B两点，点P在AB上.
(1)试找出∠1，∠2，∠3之间的关系并说出理由；
(2)如果点P在A，B两点之间运动，问∠1，∠2，∠3之间的关系是否发生变化？
(3)如果点P在A，B两点外侧运动，试探究∠1，∠2，∠3之间的关系(点P和A，B不重合).
相关试题
