【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

参考答案:
【答案】(1)∠1+∠2=∠3,理由见解析;(2)∠1+∠2=∠3,不变;(3)∠1-∠2=∠3或∠2-∠1=∠3,理由见解析.
【解析】试题分析:(1)过点P作l1的平行线,根据平行线的性质进行解题.(2)(3)都是同样的道理.
试题解析:(1)∠1+∠2=∠3.
理由:过点P作l1的平行线PQ.
∵l1∥l2,
∴l1∥l2∥PQ.
∴∠1=∠4,∠2=∠5.
∵∠4+∠5=∠3,
∴∠1+∠2=∠3.
(2)∠1+∠2=∠3不变.
(3)∠1-∠2=∠3或∠2-∠1=∠3.
理由:①当点P在下侧时,如图,过点P作l1的平行线PQ.
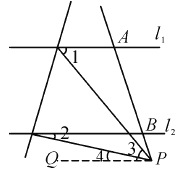
∵l1∥l2,
∴l1∥l2∥PQ.
∴∠2=∠4,∠1=∠3+∠4.
∴∠1-∠2=∠3.
②当点P在上侧时,同理可得∠2-∠1=∠3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在△ABC中,E是BC边上一点,沿AE折叠,点B恰好落在AC边上的点D处,若∠BAC=60°,BE=CD,则∠AED=______ 度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=
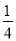 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在扇形AOB中,OA、OB是半径,且OA=4,∠AOB=120°.点P是弧AB上的一个动点,连接AP、BP,分别作OC⊥PA,OD⊥PB,垂足分别为C、D,连接CD.
(1)如图①,在点P的移动过程中,线段CD的长是否会发生变化?若不发生变化,请求出线段CD的长;若会发生变化,请说明理由;
(2)如图②,若点M、N为
 的三等分点,点I为△DOC的外心.当点P从点M运动到N点时,点I所经过的路径长为__________.(直接写出结果)
的三等分点,点I为△DOC的外心.当点P从点M运动到N点时,点I所经过的路径长为__________.(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=
 (x>0)的表达式;
(x>0)的表达式;(2)求证:AD=BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使⊙O经过A、C两点,且圆心落在AB边上;
(要求:尺规作图,保留作图痕迹,不写作法.)
(2)求证:BC是(1)中所作⊙O的切线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是关于x的方程
 =0的两个实数根.
=0的两个实数根.(1)求m的值;
(2)连接CD,试探索:AC、BC、CD三者之间的等量关系,并说明理由;
(3)若CD=
 ,求AC、BC的长.
,求AC、BC的长.
相关试题

