【题目】如图,在扇形AOB中,OA、OB是半径,且OA=4,∠AOB=120°.点P是弧AB上的一个动点,连接AP、BP,分别作OC⊥PA,OD⊥PB,垂足分别为C、D,连接CD.
(1)如图①,在点P的移动过程中,线段CD的长是否会发生变化?若不发生变化,请求出线段CD的长;若会发生变化,请说明理由;
(2)如图②,若点M、N为![]() 的三等分点,点I为△DOC的外心.当点P从点M运动到N点时,点I所经过的路径长为__________.(直接写出结果)
的三等分点,点I为△DOC的外心.当点P从点M运动到N点时,点I所经过的路径长为__________.(直接写出结果)

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)先连接AB,因为CD是△PAB的中位线,所以CD=![]() 因为AB长度不变,即CD长度不变,根据OA=4,∠AOB=120°,利用解直角三角形的方法求出AB,再根据中位线的性质即可求出CD,
因为AB长度不变,即CD长度不变,根据OA=4,∠AOB=120°,利用解直角三角形的方法求出AB,再根据中位线的性质即可求出CD,
(2)因为CD是△PAB的中位线,根据中位线的性质CD∥AB,因为点I是△DOC的外心,所以点I在CD的垂直平分线上,然后求出点I运动路线是以O为圆心,OI为半径,圆心角60°所对的弧长,利用弧长公式求解.
试题解析:∵OA=OB,OH⊥AB,
∴AH=BH=![]() AB,∠AOH=
AB,∠AOH=![]() ∠AOB=60°,
∠AOB=60°,
在Rt△AOH中,
∵∠OAH=30°,
∴OH=![]() =2,
=2,
∴在Rt△AOH,由勾股定理得AH=![]() =
=![]() ,
,
∴AB=![]() ,
,
∴CD=![]() ,
,
(2)![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在函数
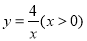 图像上,过点A作x轴和y轴的平行线分别交函数
图像上,过点A作x轴和y轴的平行线分别交函数 图像于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数
图像于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数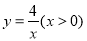 图像上运动时,
图像上运动时,
(1)设点A横坐标为a,则点B的坐标为 ,点C的坐标为 (用含a的字母表示);
(2)△ABC的面积是否发生变化?若不变,求出△ABC的面积,若变化,请说明理由;
(3)请直接写出BD与CE满足的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在△ABC中,E是BC边上一点,沿AE折叠,点B恰好落在AC边上的点D处,若∠BAC=60°,BE=CD,则∠AED=______ 度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=
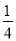 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
 (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.(1)直接写出一次函数y=kx+b的表达式和反比例函数y=
 (x>0)的表达式;
(x>0)的表达式;(2)求证:AD=BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠A=25°,∠B=40°.
(1)求作:⊙O,使⊙O经过A、C两点,且圆心落在AB边上;
(要求:尺规作图,保留作图痕迹,不写作法.)
(2)求证:BC是(1)中所作⊙O的切线.

相关试题

