【题目】已知CD是经过∠BCA顶点C的一条直线,CA=CB.E、F分别是直线CD上两点,且∠BEC=∠CFA=∠![]() .
.
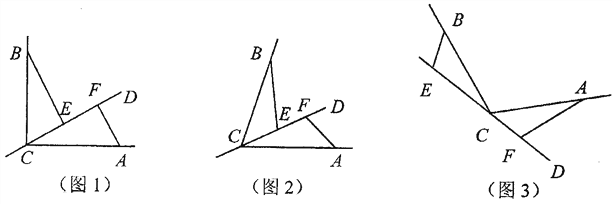
(1)若直线CD经过∠BCA的内部,且E、F在射线CD上,请解决下面问题:
①如图1若∠BCA=90°,∠![]() =90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
=90°、探索三条线段EF、BE、AF的数量关系并证明你的结论.
②如图2,若0°<∠BCA<180°, 请添加一个关于∠![]() 与∠BCA关系的条件___ ____使①中的结论仍然成立;
与∠BCA关系的条件___ ____使①中的结论仍然成立;
(2)如图3,若直线CD经过∠BCA的外部,∠![]() =∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
=∠BCA,请写出三条线段EF、BE、AF的数量关系并证明你的结论.
参考答案:
【答案】(1)①EF、BE、AF的数量关系: ![]() (相关等式均可,证明详见解析; ②∠
(相关等式均可,证明详见解析; ②∠![]() 与∠BCA关系:∠
与∠BCA关系:∠ ![]() +∠BCA=180°(或互补,相关等式均可);(2)EF、BE、AF的数量关系:
+∠BCA=180°(或互补,相关等式均可);(2)EF、BE、AF的数量关系: ![]() (相关等式均可) ,证明详见解析.
(相关等式均可) ,证明详见解析.
【解析】试题分析:(1)①求出∠BEC=∠AFC=90°,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可;.
②求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可;.
(2)求出∠BEC=∠AFC,∠CBE=∠ACF,根据AAS证△BCE≌△CAF,推出BE=CF,CE=AF即可.
试题解析:(1)①如图1中,.
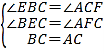 .
.
E点在F点的左侧,.
∵BE⊥CD,AF⊥CD,∠ACB=90°,.
∴∠BEC=∠AFC=90°,.
∴∠BCE+∠ACF=90°,∠CBE+∠BCE=90°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
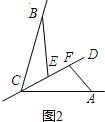 ,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
②∠α+∠ACB=180°时,①中两个结论仍然成立;.
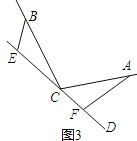
证明:如图2中,.
 .
.
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,.
∴∠CBE=∠ACF,.
在△BCE和△CAF中,.
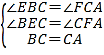 ,.
,.
∴△BCE≌△CAF(AAS),.
∴BE=CF,CE=AF,.
∴EF=CF-CE=BE-AF,.
当E在F的右侧时,同理可证EF=AF-BE,.
∴EF=|BE-AF|;
(2)EF=BE+AF..
理由是:如图3中,.
 .
.
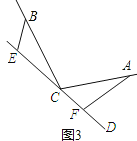
∵∠BEC=∠CFA=∠a,∠a=∠BCA,.
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,.
∴∠EBC+∠BCE=∠BCE+∠ACF,.
∴∠EBC=∠ACF,.
在△BEC和△CFA中,.
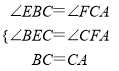 ,.
,.
∴△BEC≌△CFA(AAS),.
∴AF=CE,BE=CF,.
∵EF=CE+CF,.
∴EF=BE+AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,过O点作EF∥BC,交AB于E,交AC于F.
(1)判断△BEO的形状,并说明理由.
(2)若AB=5cm,AC=4cm,求△AEF的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】目前,我区正在实施的“同城一体化”工程进展顺利区招投标中心在对观光路工程招标时,接到甲、乙两个工程队的投标书,甲、乙施工一天的工程费用分别为1.5万元和1.1万元,区招投标中心根据甲、乙两队的投标书测算,应有三种施工方案:
(1)甲队单独做这项工程刚好如期完成;
(2)乙队单独做这项工程,要比规定日期多5天;
(3)若甲、乙两队合作4天后,余下的工程由乙队单独做,也正好如期完成.
在确保如期完成的情况下,你认为哪种方案最节省工程款,通过计算说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程由甲乙两队合做
 天完成,厂家需付甲乙两队共
天完成,厂家需付甲乙两队共 元;乙丙两队合做
元;乙丙两队合做 天完成,厂家需付乙丙两队共
天完成,厂家需付乙丙两队共 元;甲丙两队合做
元;甲丙两队合做 天完成全部工程的
天完成全部工程的 ,厂家需付甲丙两队共
,厂家需付甲丙两队共 元.
元.(1)求甲、乙、丙各队单独完成全部工程各需多少天?
(2)若要求不超过
 天完成全啊工程,问可由哪队单独完成此项工程花钱最少?
天完成全啊工程,问可由哪队单独完成此项工程花钱最少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的,∠BAC=90°,AB=6,AC=8,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为(
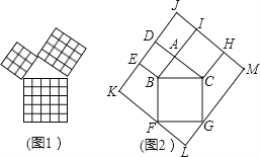
A. 360 B. 400 C. 440 D. 484
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在函数
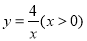 图像上,过点A作x轴和y轴的平行线分别交函数
图像上,过点A作x轴和y轴的平行线分别交函数 图像于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数
图像于点B、C,直线BC与坐标轴的交点为D、E.当点A在函数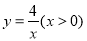 图像上运动时,
图像上运动时,
(1)设点A横坐标为a,则点B的坐标为 ,点C的坐标为 (用含a的字母表示);
(2)△ABC的面积是否发生变化?若不变,求出△ABC的面积,若变化,请说明理由;
(3)请直接写出BD与CE满足的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在△ABC中,E是BC边上一点,沿AE折叠,点B恰好落在AC边上的点D处,若∠BAC=60°,BE=CD,则∠AED=______ 度.

相关试题

