【题目】已知关于a的方程2(a﹣2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使![]() =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长.
参考答案:
【答案】(1)a=8, b=3;(2)图详见解析,7或10.
【解析】
(1)根据同解方程,可得两个方程的解相同,根据第一个方程的解,可求出第二个方程中的b;
(2)分类讨论,P在线段AB上,根据![]() ,可求出PB的长,根据Q是PB线段PB的中点,可得PQ的长,根据线段的和差,可得AQ;P在线段AB的延长线上,根据
,可求出PB的长,根据Q是PB线段PB的中点,可得PQ的长,根据线段的和差,可得AQ;P在线段AB的延长线上,根据![]() ,可求出PB的长,根据Q是PB线段PB的中点,可得BQ的长,根据线段的和差,可得AQ.
,可求出PB的长,根据Q是PB线段PB的中点,可得BQ的长,根据线段的和差,可得AQ.
(1)2(a﹣2)=a+4,
2a﹣4=a+4
a=8.
∵x=a=8,
把x=8代入方程2(x﹣3)﹣b=7,
∴2(8﹣3)﹣b=7,
b=3;
(2)①如图:
![]()
点P在线段AB上,![]() =3,
=3,
AB=3PB,AB=AP+PB=3PB+PB=4PB=8,
PB=2,Q是PB的中点,PQ=BQ=1,
AQ=AB﹣BQ=8﹣1=7,
②如图:
![]()
点P在线段AB的延长线上,![]() =3,
=3,
PA=3PB,PA=AB+PB=3PB,
AB=2PB=8,
PB=4,
Q是PB的中点,BQ=PQ=2,
AQ=AB+BQ=8+2=10.
综上所述:AQ的长为7或10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, 两点在数轴上,点
两点在数轴上,点 表示的数为-10,点
表示的数为-10,点 到点
到点 的距离是点
的距离是点 到点
到点 距离的3倍,点
距离的3倍,点 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点 向右运动.点
向右运动.点 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点 向右运动(点
向右运动(点 、
、 同时出发)
同时出发)
(1)数轴上点
 对应的数是______.
对应的数是______.(2)经过几秒,点
 、点
、点 分别到原点
分别到原点 的距离相等.
的距离相等. -
科目: 来源: 题型:
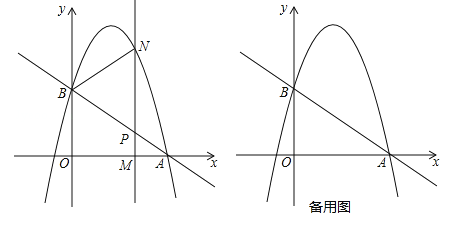
查看答案和解析>>【题目】如图,抛物线y=﹣
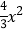 +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)在对称轴的左侧是否存在点M使四边形OMPB的面积最大,如果存在求点M的坐标;不存在请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
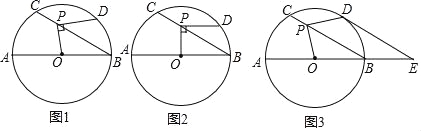
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当
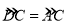 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=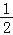 AB,连接DE.
AB,连接DE.①求证:DE是⊙O的切线;
②求PC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=
 ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索:
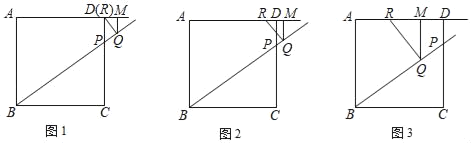 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 垂直平分
垂直平分 ,分别交
,分别交 、
、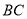 于点
于点 、
、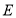 ,
, 垂直平分
垂直平分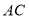 ,分别交
,分别交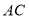 ,
,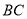 于点
于点 、
、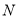 .
.⑴如图①,若
 ,求
,求 的度数;
的度数;⑵如图②,若
 ,求
,求 的度数;
的度数;⑶若

 ,直接写出用
,直接写出用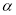 表示
表示 大小的代数式.
大小的代数式.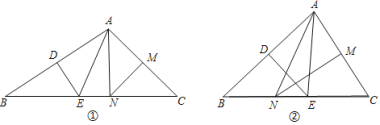
相关试题

