【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
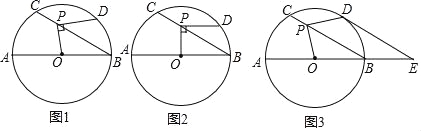
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当![]() 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=![]() AB,连接DE.
AB,连接DE.
①求证:DE是⊙O的切线;
②求PC的长.
参考答案:
【答案】(1)![]() (2)①证明见解析②3
(2)①证明见解析②3![]() ﹣3
﹣3
【解析】
试题分析:(1)根据题意首先得出半径长,再利用锐角三角三角函数关系得出OP,PD的长;
(2)①首先得出△OBD是等边三角形,进而得出∠ODE=∠OFB=90°,求出答案即可;
②首先求出CF的长,进而利用直角三角形的性质得出PF的长,进而得出答案.
试题解析:(1)如图2,连接OD,
∵OP⊥PD,PD∥AB,
∴∠POB=90°,
∵⊙O的直径AB=12,
∴OB=OD=6,
在Rt△POB中,∠ABC=30°,
∴OP=OBtan30°=6×![]() =2
=2![]() ,
,
在Rt△POD中,
PD=![]() =
=![]() =
=![]() ;
;
(2)①如图3,连接OD,交CB于点F,连接BD,
∵![]() ,
,
∴∠DBC=∠ABC=30°,
∴∠ABD=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴OD⊥FB,
∵BE=![]() AB,
AB,
∴OB=BE,
∴BF∥ED,
∴∠ODE=∠OFB=90°,
∴DE是⊙O的切线;
②由①知,OD⊥BC,
∴CF=FB=OBcos30°=6×![]() =3
=3![]() ,
,
在Rt△POD中,OF=DF,
∴PF=![]() DO=3(直角三角形斜边上的中线,等于斜边的一半),
DO=3(直角三角形斜边上的中线,等于斜边的一半),
∴CP=CF﹣PF=3![]() ﹣3.
﹣3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类
A
B
C
D
E
出行方式
共享单车
步行
公交车
的士
私家车
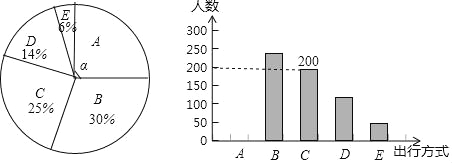
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解并在括号内填注理由:
如图,已知AB∥CD,∠1=∠2,试说明EP∥FQ.
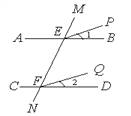
证明:∵AB∥CD,
∴∠MEB=∠MFD(_____________)
又∵∠1=∠2,
∴∠MEB-∠1=∠MFD-∠2,
即∠MEP=∠______
∴EP∥____.(_______________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M(2x﹣4,x2+2)在y轴上,则点M的坐标为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A(0,y1),B(﹣3,y2),C(3,y3)为二次函数y=﹣x2+4x﹣k的图象上的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
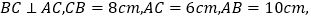 那么点A到BC的距离是_____,点B到AC的距离是_______,点A、B两点的距离是_____,点C到AB的距离是________.
那么点A到BC的距离是_____,点B到AC的距离是_______,点A、B两点的距离是_____,点C到AB的距离是________.设
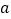 、b、c为平面上三条不同直线,
、b、c为平面上三条不同直线,①若
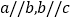 ,则a与c的位置关系是_________;
,则a与c的位置关系是_________;②若
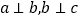 ,则a与c的位置关系是________;
,则a与c的位置关系是________;③若
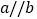 ,
,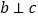 ,则a与c的位置关系是________.
,则a与c的位置关系是________.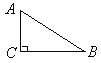
-
科目: 来源: 题型:
查看答案和解析>>【题目】 下列命题中,是真命题的是( )
A.等腰三角形都相似B.等边三角形都相似
C.锐角三角形都相似D.直角三角形都相似
相关试题

