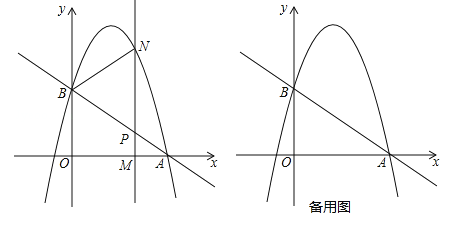
【题目】如图,抛物线y=﹣![]() +bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
+bx+c过点A(3,0),B(0,2).M(m,0)为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N.
(1)求直线AB的解析式和抛物线的解析式;
(2)如果点P是MN的中点,那么求此时点N的坐标;
(3)在对称轴的左侧是否存在点M使四边形OMPB的面积最大,如果存在求点M的坐标;不存在请说明理由.
参考答案:
【答案】(1)AB的解析式为y=﹣![]() x+2,抛物线解析式为y=﹣
x+2,抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;(2)N点坐标为(
x+2;(2)N点坐标为(![]() );(3)不存在.
);(3)不存在.
【解析】试题分析:(1)用待定系数法分别求出直线AB的解析式和抛物线的解析式即可;(2)根据题意可得N(m,﹣![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),即可得NP=﹣
m+2),即可得NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,再由NP=PM,可得方程﹣
m+2,再由NP=PM,可得方程﹣![]() m2+4m=﹣
m2+4m=﹣![]() m+2,解方程即可求得m的值,从而求得点N的坐标;(3)在对称轴的左侧不存在点M使四边形OMPB的面积最大,根据题意和已知条件求出S梯形OMPB和m的函数关系式,利用二次函数的性质判定即可.
m+2,解方程即可求得m的值,从而求得点N的坐标;(3)在对称轴的左侧不存在点M使四边形OMPB的面积最大,根据题意和已知条件求出S梯形OMPB和m的函数关系式,利用二次函数的性质判定即可.
试题解析:
(1)设直线AB的解析式为y=px+q,
把A(3,0),B(0,2)代入得![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣![]() x+2;
x+2;
把A(3,0),B(0,2)代入y=﹣![]() +bx+c得
+bx+c得 ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵M(m,0),MN⊥x轴,
∴N(m,﹣![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),
m+2),
∴NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,
m+2,
而NP=PM,
∴﹣![]() m2+4m=﹣
m2+4m=﹣![]() m+2,解得m1=3(舍去),m2=
m+2,解得m1=3(舍去),m2=![]() ,
,
∴N点坐标为(![]() ,
,![]() );
);
(3)在对称轴的左侧不存在点M使四边形OMPB的面积最大,理由如下:
B(0,2),M(m,0),MN⊥x轴,
∴P(m,﹣![]() m+2),
m+2),
S梯形OMPB=![]() (PM+OB)OM=
(PM+OB)OM=![]() (﹣
(﹣![]() m+2+2)m
m+2+2)m
=﹣![]() m2+2m
m2+2m
=﹣![]() (m﹣3)2+3
(m﹣3)2+3
∵对称轴是x=﹣![]() =
=![]() ,M在对称轴的左侧,
,M在对称轴的左侧,
∴0<m<![]() ,
,
∴m的值无法确定,
在对称轴的左侧不存在点M使四边形OMPB的面积最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点C在直线AB上,且线段AB=16,若AB:BC=8:3,E是AC的中点,D是AB的中点,则线段DE=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在同一平面内有四个点A、B、C、D.
(1)请按要求作出图形(注:此题作图不需要写出画法和结论);
①作射线AC;
②作直线BD,交射线AC相于点O;
③分别连接AB、AD;
④求作一条线段MN,使其等于AC﹣AB(用尺规作图,保留作图痕迹).
(2)观察B、D两点间的连线,我们容易判断出线段AB+AD>BD,理由是 ;
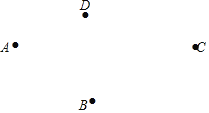
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,
, 两点在数轴上,点
两点在数轴上,点 表示的数为-10,点
表示的数为-10,点 到点
到点 的距离是点
的距离是点 到点
到点 距离的3倍,点
距离的3倍,点 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点 向右运动.点
向右运动.点 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点 向右运动(点
向右运动(点 、
、 同时出发)
同时出发)
(1)数轴上点
 对应的数是______.
对应的数是______.(2)经过几秒,点
 、点
、点 分别到原点
分别到原点 的距离相等.
的距离相等. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,⊙O的直径AB=12,P是弦BC上一动点(与点B,C不重合),∠ABC=30°,过点P作PD⊥OP交⊙O于点D.
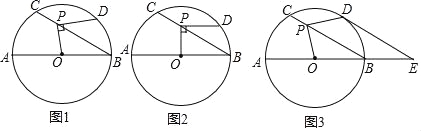
(1)如图2,当PD∥AB时,求PD的长;
(2)如图3,当
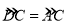 时,延长AB至点E,使BE=
时,延长AB至点E,使BE=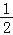 AB,连接DE.
AB,连接DE.①求证:DE是⊙O的切线;
②求PC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于a的方程2(a﹣2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使
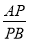 =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
相关试题

