【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
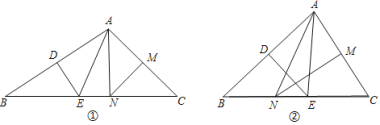
⑴如图①,若![]() ,求
,求![]() 的度数;
的度数;
⑵如图②,若![]() ,求
,求![]() 的度数;
的度数;
⑶若![]()
![]() ,直接写出用
,直接写出用![]() 表示
表示![]() 大小的代数式.
大小的代数式.
参考答案:
【答案】(1)∠EAN=44°;(2)∠EAN=16°;(3)当0<α<90°时,∠EAN=180°-2α;当α>90°时,∠EAN=2α-180°.
【解析】
(1)根据线段垂直平分线上的点到线段两端点的距离相等可得AE=BE,再根据等边对等角可得∠BAE=∠B,同理可得,∠CAN=∠C,然后利用三角形的内角和定理求出∠B+∠C,再根据∠EAN=∠BAC-(∠BAE+∠CAN)代入数据进行计算即可得解;
(2)同(1)的思路,最后根据∠EAN=∠BAE+∠CAN-∠BAC代入数据进行计算即可得解;
(3)根据前两问的求解,分α<90°与α>90°两种情况解答.
(1)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C),
在△ABC中,∠B+∠C=180°-∠BAC=180°-112°=68°,
∴∠EAN=∠BAC-(∠BAE+∠CAN)=112°-68°=44°;
(2)∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=180°-∠BAC=180°-82°=98°,
∴∠EAN=∠BAE+∠CAN-∠BAC=98°-82°=16°;
(3)当0<α<90°时,
∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAE+∠CAN-∠BAC=(∠B+∠C)-∠BAC,
在△ABC中,∠B+∠C=180°-∠BAC=180°-α,
∴∠EAN=∠BAE+∠CAN-∠BAC=180°-α-α=180°-2α;
当α>90°时,
∵DE垂直平分AB,
∴AE=BE,
∴∠BAE=∠B,
同理可得:∠CAN=∠C,
∴∠EAN=∠BAC-∠BAE-∠CAN=∠BAC-(∠B+∠C),
在△ABC中,∠B+∠C=180°-∠BAC=180°-α,
∴∠EAN=∠BAC-(∠BAE+∠CAN)=α-(180°-α)=2α-180°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于a的方程2(a﹣2)=a+4的解也是关于x的方程2(x﹣3)﹣b=7的解.
(1)求a、b的值;
(2)若线段AB=a,在直线AB上取一点P,恰好使
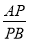 =b,点Q为PB的中点,请画出图形并求出线段AQ的长.
=b,点Q为PB的中点,请画出图形并求出线段AQ的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的2016年6月份的日历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )

A. 27 B. 51 C. 69 D. 72
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=
 ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索:
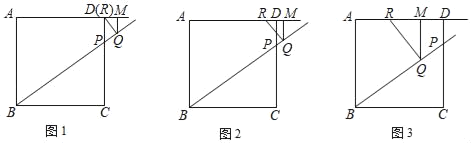 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,按照这种规律下去,第n次移动到点An,如果点An,与原点的距离不少于20,那么n的最小值是( )

A. 11B. 12C. 13D. 20
-
科目: 来源: 题型:
查看答案和解析>>【题目】以∠AOB的顶点O为端点引射线OP,使∠AOP:∠BOP=3:2,若∠AOB=20°,则∠AOP的度数为_________.
相关试题

