【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;0≤x≤
;0≤x≤![]() .
.
【解析】试题分析:(1)由正方形的性质及![]() 可求出BC=8,PC=6,由勾股定理可求出BP=10,再由△
可求出BC=8,PC=6,由勾股定理可求出BP=10,再由△![]() ∽△
∽△![]() 即可求出结论;
即可求出结论;
(2)由正方形的性质得∠A=∠ABC=∠C=90°,由MQ∥AB得∠QMR=∠A,故∠QMR=∠C;由MQ∥AB得![]() ,而∠1+∠RQM=90°,∠ABP+∠PBC=90°,故
,而∠1+∠RQM=90°,∠ABP+∠PBC=90°,故![]() ,从而△
,从而△![]() ∽△
∽△![]() .故可得出结论;
.故可得出结论;
(3)延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,通过证明
,通过证明![]() ,分别计算
,分别计算![]() 及
及![]() ,
, ![]() ,从而可得出结论.
,从而可得出结论.
试题解析:(1)由题意,得![]() ,
,![]()
在Rt△![]() 中,
中, ![]()
∴![]()
∵![]()
∴![]() ∴
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴△![]() ∽△
∽△![]()
∴![]()
∴![]()
∴![]()
(2)答: ![]() 的比值随点
的比值随点![]() 的运动没有变化
的运动没有变化
理由:如图,

∵![]() ∥
∥![]()
∴![]() ,
, ![]()
∵![]()
∴![]()
∵![]()
∴![]()
![]()
∴![]()
∴△![]() ∽△
∽△![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
∴![]() 的比值随点
的比值随点![]() 的运动没有变化,比值为
的运动没有变化,比值为![]()
(3)延长![]() 交
交![]() 的延长线于点
的延长线于点![]()
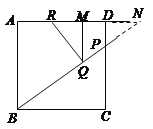
∵![]() ∥
∥![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() ∥
∥![]() ,
, ![]() ∥
∥![]()
∴![]() ∥
∥![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
又![]() ,
, ![]()
∴
∴![]()
它的定义域是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,以顶点A为圆心,AD长为半径,在AB边上截取AE=AD,用尺规作图法作出∠BAD的角平分线AG,若AD=5,DE=6,则AG的长是_________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细观察下列等式:
第1个:22﹣1=1×3
第2个:32﹣1=2×4
第3个:42﹣1=3×5
第4个:52﹣1=4×6
第5个:62﹣1=5×7
…
这些等式反映出自然数间的某种运算规律.按要求解答下列问题:
(1)请你写出第6个等式: ;
(2)设n(n≥1)表示自然数,则第n个等式可表示为 ;
(3)运用上述结论,计算:
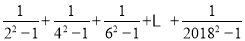 .
. -
科目: 来源: 题型:
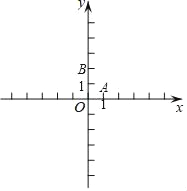
查看答案和解析>>【题目】已知在平面直角坐标系xOy(如图)中,已知抛物线y=
 +bx+c点经过A(1,0)、B(0,2).
+bx+c点经过A(1,0)、B(0,2).(1)求该抛物线的表达式;
(2)设该抛物线的对称轴与x轴的交点为C,第四象限内的点D在该抛物线的对称轴上,如果以点A、C、D所组成的三角形与△AOB相似,求点D的坐标;
(3)设点E在该抛物线的对称轴上,它的纵坐标是1,联结AE、BE,求sin∠ABE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
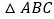 中,
中,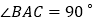 ,
,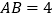 ,
,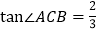 ,点D、E分别是BC、AD的中点,
,点D、E分别是BC、AD的中点,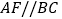 交CE的延长线于点F,则四边形AFBD的面积为______.
交CE的延长线于点F,则四边形AFBD的面积为______.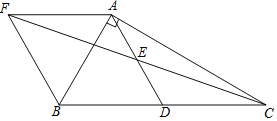
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲、乙两种商品,已知每件甲种商品的价格比每件乙种商品的价格贵10元,用350元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同.
(1)求甲、乙两种商品每件的价格各是多少元?
(2)计划购买这两种商品共50件,且投入的经费不超过3200元,那么,最多可购买多少件甲种商品?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,点A(0,0)、B(4
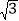 ,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )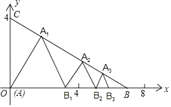
A.
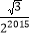 B.
B. 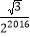 C.
C. 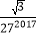 D.
D. 
相关试题

