【题目】如图,我把对角线互相垂直的四边形叫做“垂美四边形”.
(1)性质探究:如图1.已知四边形ABCD中,AC⊥BD,垂足为O,求证:AB2+CD2=AD2+BC2.
(2)解决问题:已知AB=5,BC=4,分别以△ABC的边BC和AB向外作等腰Rt△BCQ和等腰Rt△ABP.
①如图2,当∠ACB=90°,连接PQ,求PQ;
②如图3,当∠ACB≠90°,点M、N分别是AC、AP中点连接MN.若MN=![]() ,则S△ABC= .
,则S△ABC= .

参考答案:
【答案】(1)详见解析;(2)①![]() ,②
,②![]()
【解析】
(1)利用勾股定理即可得出结论;
(2)①根据SAS可证明△PBC≌△ABQ,得∠BPC=∠BAQ,得∠PDA=90°,可求出PQ的长;
②连接PC、AQ交于点D,同①可证△PBC≌△ABQ,则AQ=PC且AQ⊥PC,由MN=2![]() ,可知AQ=PC=4
,可知AQ=PC=4![]() .延长QB作AE⊥QE,求出BE的长,则答案可求出.
.延长QB作AE⊥QE,求出BE的长,则答案可求出.
解:(1)证明:如图中,

∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AB2+CD2=AD2+BC2;
(2)①如图,连接PC、AQ交于点D,
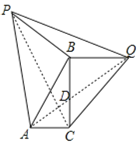
∵△ABP和△CBQ都是等腰直角三角形,
∴PB=AB,CB=BQ,∠ABP=∠CBQ=90°,
∴∠PBC=∠ABQ,
∴△PBC≌△ABQ(SAS),
∴∠BPC=∠BAQ,
又∵∠BPC+∠CPA+∠BAP=90°,
即∠BAQ+∠CPA+∠BAP=90°,
∴∠PDA=90°,
∴PC⊥AQ,
利用(1)中的结论:AP2+CQ2=AC2+PQ2
即(5![]() )2+(4
)2+(4![]() )2=32+PQ2;
)2=32+PQ2;
∴PQ=![]() .
.
②如图,连接PC、AQ交于点D,
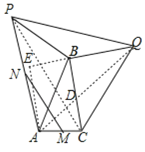
同①可证△PBC≌△ABQ(SAS),AQ=PC且AQ⊥PC,
∵M、N分别是AC、AP中点,
∴MN=![]() ,
,
∵MN=2![]() ,
,
∴AQ=PC=4![]() .
.
延长QB作AE⊥QE,
则有AE2+BE2=25,AE2+QE2=48,
∵EQ=4+BE,
∴(4+BE)2﹣BE2=23,
解得BE=![]() ,
,
∴S△ABC=![]() BC×BE=
BC×BE=![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有1个蓝球和2个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,求摸到蓝球的概率;
(2)搅匀后从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球.
求至少有1次摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,点D为AB的中点,过点D作DE∥BC交AC于E.
(1)求证:E为AC的中点;
(2)如图2,过点D作QD⊥AB交BC的延长线于Q,过点E作EP⊥AC交CB的延长线于P,连AP、AQ.若PQ=12,AP+AQ=20,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在直角坐标系中,
在直角坐标系中, 请写出
请写出 各点的坐标.
各点的坐标. 若把
若把 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到 ,写出
,写出 、
、 、
、 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形. 求出三角形ABC的面积.
求出三角形ABC的面积.
-
科目: 来源: 题型:
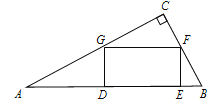
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上.
(1)求证:△ADG∽△FEB;
(2)若AG=5,AD=4,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,点B在x轴上,且
,点B在x轴上,且 .
. 求点B的坐标;
求点B的坐标; 求
求 的面积;
的面积; 在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
相关试题

