【题目】如图1,在△ABC中,点D为AB的中点,过点D作DE∥BC交AC于E.
(1)求证:E为AC的中点;
(2)如图2,过点D作QD⊥AB交BC的延长线于Q,过点E作EP⊥AC交CB的延长线于P,连AP、AQ.若PQ=12,AP+AQ=20,求DE的长.

参考答案:
【答案】(1)详见解析;(2)4
【解析】
(1)作CF∥AB交DE的延长线于点F,证明△ADE≌△CFE,根据全等三角形的性质得到AE=CE;
(2)根据线段垂直平分线的性质得到QA=QB,AP=CP,求出BC的长,根据三角形中位线定理解答即可.
(1)证明:作CF∥AB交DE的延长线于点F,
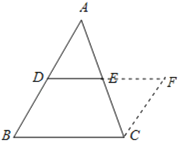
则∠A=∠FCE,
∵DE∥BC,CF∥AB,
∴四边形DBCF为平行四边形,
∴BD=CF,
∵点D为AB的中点,
∴AD=BD,
∴AD=CF,
在△ADE和△CFE中,
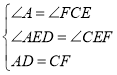 ,
,
∴△ADE≌△CFE(ASA),
∴AE=CE,即E为AC的中点;
(2)∵点D为AB的中点,QD⊥AB,
∴QA=QB,
同理,AP=CP,
∴BC=CP+BQ﹣PQ=AP+AQ﹣PQ=20﹣12=8,
∵D、E分别为AB、AC的中点,
∴DE=![]() BC=4
BC=4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD//EF,∠1+∠2=180°,
(1)若∠1=50°,求∠BAD的度数;
(2)若DG⊥AC,垂足为G,∠BAC=90°,试说明:DG平分∠ADC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有1个蓝球和2个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出1个球,求摸到蓝球的概率;
(2)搅匀后从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球.
求至少有1次摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我把对角线互相垂直的四边形叫做“垂美四边形”.
(1)性质探究:如图1.已知四边形ABCD中,AC⊥BD,垂足为O,求证:AB2+CD2=AD2+BC2.
(2)解决问题:已知AB=5,BC=4,分别以△ABC的边BC和AB向外作等腰Rt△BCQ和等腰Rt△ABP.
①如图2,当∠ACB=90°,连接PQ,求PQ;
②如图3,当∠ACB≠90°,点M、N分别是AC、AP中点连接MN.若MN=
 ,则S△ABC= .
,则S△ABC= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 在直角坐标系中,
在直角坐标系中, 请写出
请写出 各点的坐标.
各点的坐标. 若把
若把 向上平移2个单位,再向左平移1个单位得到
向上平移2个单位,再向左平移1个单位得到 ,写出
,写出 、
、 、
、 的坐标,并在图中画出平移后图形.
的坐标,并在图中画出平移后图形. 求出三角形ABC的面积.
求出三角形ABC的面积.
-
科目: 来源: 题型:
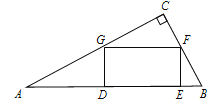
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上.
(1)求证:△ADG∽△FEB;
(2)若AG=5,AD=4,求BE的长.
相关试题

