【题目】如图,![]() ,
,![]() ,点B在x轴上,且
,点B在x轴上,且![]() .
.
![]() 求点B的坐标;
求点B的坐标;
![]() 求
求![]() 的面积;
的面积;
![]() 在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.
在y轴上是否存在P,使以A、B、P三点为顶点的三角形的面积为10?若存在,请求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)(-4,0)或(2,0);(2)6;(3)(0,![]() )或(0,
)或(0,![]() )
)
【解析】
(1)分点B在点A的左边和右边两种情况解答;
(2)利用三角形的面积公式列式计算即可得解;
(3)利用三角形的面积公式列式求出点P到x轴的距离,然后分两种情况写出点P的坐标即可.

解:(1)当点B在点A的右边时,点B的坐标为(2,0);
当点B在点A的左边时,点B的坐标为(-4,0).
所以点B的坐标为(2,0)或(-4,0).
(2)三角形ABC的面积为![]() ×3×4=6.
×3×4=6.
(3)设点P到x轴的距离为h,则
![]() ×3h=10,解得h=
×3h=10,解得h=![]() .
.
①当点P在y轴正半轴时,点P的坐标为(0,![]() );
);
②当点P在y轴负半轴时,点P的坐标为(0,-![]() ).
).
综上所述,点P的坐标为(0,![]() )或(0,-
)或(0,-![]() )
)
-
科目: 来源: 题型:
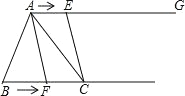
查看答案和解析>>【题目】如图,在△ABC 中,BC=6cm.射线 AG∥BC,点 E 从点 A 出发沿射线 AG 以 2cm/s 的速度运动,当点 E 先出发 1s 后,点 F 也从点 B 出发沿射线 BC 以
 cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.
cm/s 的速度运动,分别连结 AF,CE.设点 F 运动时间为 t(s),其中 t>0.(1)当 t 为何值时,∠BAF<∠BAC;
(2)当 t 为何值时,AE=CF;
(3)当 t 为何值时,S△ABF+S△ACE<S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点O是正方形ABCD两对角线的交点. 分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转
 角(0°<
角(0°<  <360°)得到正方形
<360°)得到正方形 ,如图2.
,如图2.①在旋转过程中,当∠
 是直角时,求
是直角时,求 的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)②若正方形ABCD的边长为1,在旋转过程中,求
 长的最大值和此时
长的最大值和此时 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.
图1 图2
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校计划购买一批篮球和足球,已知购买2个篮球和1个足球共需320元,购买3个篮球和2个足球共需540元.
(1)求每个篮球和每个足球的售价;
(2)如果学校计划购买这两种球共50个,总费用不超过5500元,那么最多可购买多少个足球?
-
科目: 来源: 题型:
查看答案和解析>>【题目】对
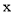 ,
, 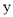 定义一种新运算
定义一种新运算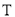 ,规定
,规定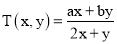 (其中
(其中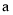 ,
, 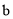 均为非零常数),这里等式右边是通常的四则运算,例:
均为非零常数),这里等式右边是通常的四则运算,例: 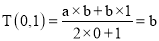 .
.已知
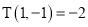 ,
, 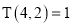 .
. (1)求
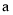 ,
, 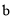 的值;
的值;(2)若关于m的不等式组
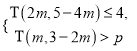 恰好有3个整数解,求实数
恰好有3个整数解,求实数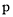 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形都是由同样大小的空心圆圈按照一定规律所组成的,其中图
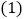 中一共有7个空心圆圈;图
中一共有7个空心圆圈;图 中一共有11个空心圆圈;图
中一共有11个空心圆圈;图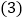 中一共有15个空心圆圈;
中一共有15个空心圆圈;
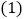 图
图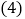 一共应有______个空心圆圈.
一共应有______个空心圆圈. 按此规律排列下去,猜想图
按此规律排列下去,猜想图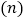 中一共有多少个空心圆圈?用含n的代数式表示
中一共有多少个空心圆圈?用含n的代数式表示 不用说理
不用说理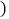 .
.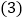 是否存在图
是否存在图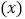 中一共有2018个空心圆圈?若存在,求出x的值;若不存在,请说明理由.
中一共有2018个空心圆圈?若存在,求出x的值;若不存在,请说明理由.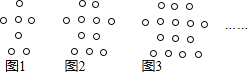
-
科目: 来源: 题型:
查看答案和解析>>【题目】网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
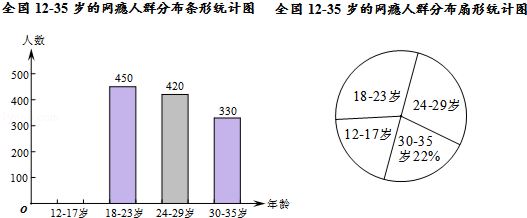
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数.
相关试题

