搜索
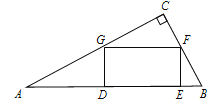
【题目】如图，在Rt△ABC中，∠C＝90°，矩形DEFG的顶点G、F分别在AC、BC上，DE在AB上．
（1）求证：△ADG∽△FEB；
（2）若AG＝5，AD＝4，求BE的长．
参考答案：
【答案】（1）证明见解析；（2）
．
【解析】分析：（1）易证∠AGD=∠B，根据∠ADG=∠BEF=90°，即可证明△ADG∽△FEB；（2）根据勾股定理和相似三角形的性质解答即可.
本题解析：
（1）∵∠C=90°，∴∠A+∠B=90°；
∵四边形DEFG是矩形，∴∠GDE=∠FED=90°，∴∠GDA=∠FED=90°；
∴∠A+∠AGD=90°，∴∠B=∠AGD且∠GDA=∠FED=90°，∴△ADG∽△FEB． ．
（2）在Rt△AGD中，∠GDA=90°由勾股定理得，AD+GD=AG, ∵AD=4，AG=5，∴GD=3，∵△ADG∽△FEB，∴ 
；
∵四边形DEFG是矩形，∴FE=DG=3；∴ 
， ∴ BE =
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在△ABC中，点D为AB的中点，过点D作DE∥BC交AC于E．
（1）求证：E为AC的中点；
（2）如图2，过点D作QD⊥AB交BC的延长线于Q，过点E作EP⊥AC交CB的延长线于P，连AP、AQ．若PQ＝12，AP+AQ＝20，求DE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，我把对角线互相垂直的四边形叫做“垂美四边形”．
（1）性质探究：如图1．已知四边形ABCD中，AC⊥BD，垂足为O，求证：AB2+CD2＝AD2+BC2．
（2）解决问题：已知AB＝5，BC＝4，分别以△ABC的边BC和AB向外作等腰Rt△BCQ和等腰Rt△ABP．
①如图2，当∠ACB＝90°，连接PQ，求PQ；
②如图3，当∠ACB≠90°，点M、N分别是AC、AP中点连接MN．若MN＝
，则S△ABC＝ ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
在直角坐标系中，
请写出各点的坐标．
若把向上平移2个单位，再向左平移1个单位得到
，写出
、
、
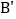的坐标，并在图中画出平移后图形．
求出三角形ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
，点B在x轴上，且
．
求点B的坐标；
求
的面积；
在y轴上是否存在P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图点A（a，0）在x轴负半轴，点B（b，0）在x轴正半轴，点C（0，c）在y轴正半轴，且
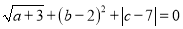．（1）如图1，求S△ABC；
（2）如图2，若点D（0，5），BD的延长线交AC于E，求∠AEB；
（3）如图3，在（2）的条件下，将线段BA绕点B逆时针旋转90°至线段BF，连接EF，试探究EA，EB，EF之间有怎样的数量关系，并证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在菱形ABCD中，M是BC边上的点（不与B，C两点重合），AB=AM，点B关于直线AM对称的点是N，连接DN，设∠ABC，∠CDN的度数分别为
，
，则关于的函数解析式是_______________________________．
相关试题
