【题目】如图,已知点A(﹣3,0),二次函数y=ax2+bx+ ![]() 的对称轴为直线x=﹣1,其图象过点A与x轴交于另一点B,与y轴交于点C.
的对称轴为直线x=﹣1,其图象过点A与x轴交于另一点B,与y轴交于点C.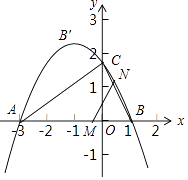
(1)求二次函数的解析式,写出顶点坐标;
(2)动点M,N同时从B点出发,均以每秒2个三位长度的速度分别沿△ABC的BA,BC边上运动,设其运动的时间为t秒,当其中一个点到达终点时,另一个点也随之停止运动,连结MN,将△BMN沿MN翻折,若点B恰好落在抛物线弧上的B′处,试求t的值及点B′的坐标;
(3)在(2)的条件下,Q为BN的中点,试探究坐标轴上是否存在点P,使得以B,Q,P为顶点的三角形与△ABC相似?如果存在,请求出点P的坐标;如果不存在,试说明理由.
参考答案:
【答案】
(1)
解:由题意得 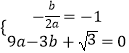 ,
,
解得 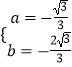 ,
,
二次函数的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+
x+ ![]()
配方得y=﹣ ![]() (x+1)2+
(x+1)2+ ![]() ,
,
顶点坐标为(﹣1, ![]() ),
),
(2)
解:如图1
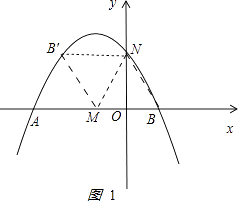 ,
,
由题意知OA=3,OB=1,ON= ![]() ,
,
∴∠CBA=60°,
又∵BM=BN,
∴△MBN是正三角形,
∴M(1﹣2t,0),N(1﹣t, ![]() t).
t).
将△BMN沿MN翻折后,得
B′N=BN=2t,∠B′NM=∠BMN=60°,
∴B′N∥BM,
∴B′(1﹣3t, ![]() t),
t),
又点B′在抛物线上,
∴ ![]() t=﹣
t=﹣ ![]() (1﹣3t)2﹣
(1﹣3t)2﹣ ![]() (1﹣3t)+
(1﹣3t)+ ![]() ,
,
化简,得9t2﹣9t=0,解得t=0(不符合题意,舍)t=1,
t=1时,1﹣3t=﹣2, ![]() t=
t= ![]() ,
,
∴B′(﹣2, ![]() );
);
(3)
解:由题意可得△ABC是直角三角形,且∠BAC=30°,∠ABC=60°.又Q( ![]() ,
, ![]() ).
).
①如图2
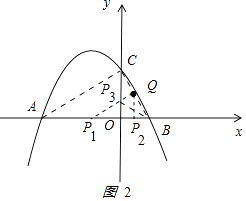 ,
,
由题意知OA=3,OB=1,
P在x轴上时,过Q作P1Q⊥BQ交x轴于P1点,
∵P1Q∥AC,
∴1BQ∽△ABC,
![]() =
= ![]() =
= ![]() ,
,
解得P1B=2,OP1=1,P1(﹣1,0);
过Q作P2Q⊥x轴于P2,
∵∠P2BQ=∠CBA,∠QPB=∠ACB,
∴QBP2∽△ABC,
![]() =
= ![]() ,
,
解得BP2= ![]() ,OP2=
,OP2= ![]() ,
,
P2( ![]() ,0);
,0);
P在x轴的其它位置时,△PBQ不可能为直角三角形,不可能与△ABC相似;
②同理,当P在y轴上时,作P3Q⊥BQ交y轴于P3,
∵∠P3BQ=∠BAC=∠P3BO=30°,∠P3QB=∠ACB=90°,
∴△BP3Q∽△ABC.
∵tan∠P3BO= ![]() =
= ![]() ,P3O=
,P3O= ![]() ,
,
P3(0, ![]() ).
).
B作P4B⊥BQ交y于P4,但 ![]() ≠
≠ ![]() ,
,
∴△QBP4Y与△ABC不相似,P在y轴上其它位置时,△PQB不为直角三角形,不能与△ABC相似;
综上所述:坐标轴上存在点P,使得以B,Q,P为顶点的三角形与△ABC相似,P点坐标为(﹣1,0),( ![]() ,0),(0,
,0),(0, ![]() ).
).
【解析】(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;(2)根据等边三角形的判定,可得△MBN是正三角形,根据翻折的性质,可得B′N,∠B′NM,根据平行线的判定,可得B′的纵坐标,根据点的坐标满足函数解析式,可得关于t的方程,根据解方程,可得t,可得B′的坐标;(3)根据相似三角形的判定与性质,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点P为BC的中点,连接EP,AD.
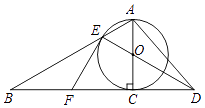
(1)求证:PE是⊙O的切线;
(2)若⊙O的半径为3,∠B=30°,求P点到直线AD的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是小华同学一个学期数学成绩的记录.根据表格提供的信息,回答下列的问题:
考试类别
平时考试
期中考试
期末考试
第一单元
第二单元
第三单元
第四单元
成绩(分)
85
78
90
91
90
94
(1)小明6次成绩的众数是 ,中位数是 ;
(2)求该同学这个同学这一学期平时成绩的平均数;
(3)总评成绩权重规定如下:平时成绩占20%,期中成绩占30%,期末成绩占50%,请计算出小华同学这一个学期的总评成绩是多少分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在Rt△ABC中,斜边AB=10,sinA=
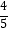 ,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.
,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.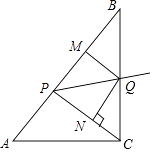
(1)当AP=CP时,求QP;
(2)若四边形PMQN为菱形,求CQ;
(3)探究:AP为何值时,四边形PMQN与△BPQ的面积相等? -
科目: 来源: 题型:
查看答案和解析>>【题目】2022年将在北京﹣﹣张家口举办冬季奥运会,北京将成为世界上第一个既举办夏季奥运会,又举办冬季奥运会的城市,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练,他们的身高(单位:cm)如表所示:
队员1
队员2
队员3
队员4
队员5
队员6
甲组
176
177
175
176
177
175
乙组
178
175
170
174
183
176
设两队队员身高的平均数依次为
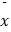 甲 ,
甲 , 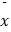 乙 , 方差依次为S甲2 , S乙2 , 下列关系中正确的是( )
乙 , 方差依次为S甲2 , S乙2 , 下列关系中正确的是( )
A.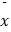 甲=
甲= 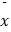 乙 , S甲2<S乙2
乙 , S甲2<S乙2
B.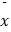 甲=
甲= 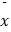 乙,S甲2>S乙2
乙,S甲2>S乙2
C.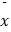 甲<
甲< 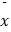 乙 , S甲2<S乙2
乙 , S甲2<S乙2
D.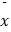 甲>
甲> 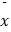 乙 , S甲2>S乙2
乙 , S甲2>S乙2 -
科目: 来源: 题型:
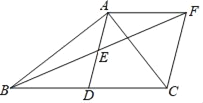
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论;
(3)在(2)的情况下,点M在AC线段上移动,请直接回答,当点M移动到什么位置时,MB+MD有最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,正确表示函数y=kx+k(k≠0)与y=
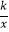 (k≠0)的图象的是( )
(k≠0)的图象的是( )
A.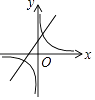
B.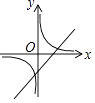
C.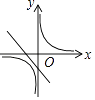
D.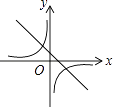
相关试题

