搜索
【题目】在同一平面直角坐标系中，正确表示函数y=kx+k（k≠0）与y= 
（k≠0）的图象的是（ ）
A.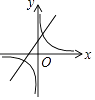
B.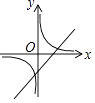
C.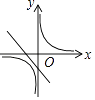
D.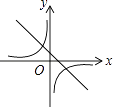
参考答案：
【答案】A
【解析】解：①当k＞0时，y=kx+k过一、二、三象限；y= 
（k≠0）过一、三象限； ②当k＜0时，y=kx+k过二、三、四象象限；y= （k≠0）过二、四象限．
观察图形可知，只有A选项符合题意．
故选：A．
【考点精析】解答此题的关键在于理解一次函数的图象和性质的相关知识，掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A（﹣3，0），二次函数y=ax2+bx+
的对称轴为直线x=﹣1，其图象过点A与x轴交于另一点B，与y轴交于点C．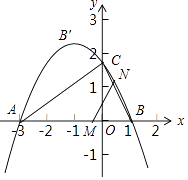
（1）求二次函数的解析式，写出顶点坐标；
（2）动点M，N同时从B点出发，均以每秒2个三位长度的速度分别沿△ABC的BA，BC边上运动，设其运动的时间为t秒，当其中一个点到达终点时，另一个点也随之停止运动，连结MN，将△BMN沿MN翻折，若点B恰好落在抛物线弧上的B′处，试求t的值及点B′的坐标；
（3）在（2）的条件下，Q为BN的中点，试探究坐标轴上是否存在点P，使得以B，Q，P为顶点的三角形与△ABC相似？如果存在，请求出点P的坐标；如果不存在，试说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】2022年将在北京﹣﹣张家口举办冬季奥运会，北京将成为世界上第一个既举办夏季奥运会，又举办冬季奥运会的城市，某校开设了冰球选修课，12名同学被分成甲、乙两组进行训练，他们的身高（单位：cm）如表所示：
队员1
队员2
队员3
队员4
队员5
队员6
甲组
176
177
175
176
177
175
乙组
178
175
170
174
183
176
设两队队员身高的平均数依次为
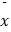甲 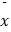， 乙 ， 方差依次为S甲2 ， S乙2 ， 下列关系中正确的是（ ）
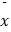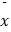A. 甲= 乙 ， S甲2＜S乙2
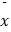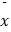B. 甲= 乙，S甲2＞S乙2
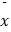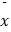C. 甲＜ 乙 ， S甲2＜S乙2
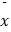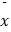D. 甲＞ 乙 ， S甲2＞S乙2 -
科目： 来源： 题型：
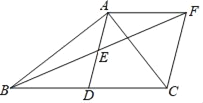
查看答案和解析>>【题目】如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．
（1）求证：△AEF≌△DEB；
（2）若∠BAC=90°，试判断四边形ADCF的形状，并证明你的结论；
（3）在（2）的情况下，点M在AC线段上移动，请直接回答，当点M移动到什么位置时，MB+MD有最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，直线y=﹣
x+4与x轴、y轴分别交于点A、点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．（1）求AB的长和点C的坐标；
（2）求直线CD的解析式；
（3）y轴上是否存在一点P，使得S△PAB=
，若存在，请求出点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料： 小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：
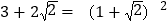，善于思考的小明进行了以下探索：设
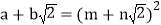（其中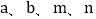
均为整数），则有
．∴
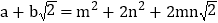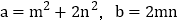．这样小明就找到了一种把部分
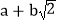的式子化为平方式的方法．请你仿照小明的方法探索并解决下列问题：
当
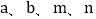均为正整数时，若
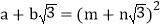，用含m、n的式子分别表示
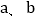，得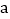
＝ ，
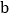＝ ；（2）利用所探索的结论，找一组正整数
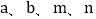，填空： ＋ ＝( ＋ 
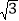)2；（3）若
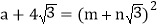，且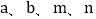均为正整数，求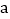的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读以下材料：
对数的创始人是苏格兰数学家纳皮尔（J．Nplcr，1550﹣1617年），纳皮尔发明对数是在指数书写方式之前，直到18世纪瑞士数学家欧拉（Evlcr，1707﹣1783年）才发现指数与对数之间的联系．
对数的定义：一般地，若ax=N（a＞0，a≠1），那么x叫做以a为底N的对数，记作：x=logaN．比如指数式24=16可以转化为4=log216，对数式2=log525可以转化为52=25．
我们根据对数的定义可得到对数的一个性质：loga（MN）=logaM+logaN（a＞0，a≠1，M＞0，N＞0）；理由如下：
设logaM=m，logaN=n，则M=am，N=an
∴MN=aman=am+n，由对数的定义得m+n=loga（MN）
又∵m+n=logaM+logaN
∴loga（MN）=logaM+logaN
解决以下问题：
（1）将指数43=64转化为对数式_____；
（2）证明loga
=logaM﹣logaN（a＞0，a≠1，M＞0，N＞0）（3）拓展运用：计算log32+log36﹣log34=_____．
相关试题
