【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下五个结论:①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤![]() .当∠EPF在△ABC内绕顶点P旋转时(点E不与点A、B重合),上述结论中始终正确的序号有 .
.当∠EPF在△ABC内绕顶点P旋转时(点E不与点A、B重合),上述结论中始终正确的序号有 .

参考答案:
【答案】①②③⑤
【解析】试题分析:根据等腰直角三角形的性质可得AP⊥BC,AP=PC,∠EAP=∠C=45°,根据同角的余角相等求出∠APE=∠CPF,判定②正确,然后利用“角边角”证明△APE和△CPF全等,根据全等三角形的可得AE=CF,判定①正确,再根据等腰直角三角形的定义得到△EFP是等腰直角三角形,判定③正确;根据等腰直角三角形的斜边等于直角边的![]() 倍表示出EF,可知EF随着点E的变化而变化,判定④错误,根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半,判定⑤正确.
倍表示出EF,可知EF随着点E的变化而变化,判定④错误,根据全等三角形的面积相等可得△APE的面积等于△CPF的面积相等,然后求出四边形AEPF的面积等于△ABC的面积的一半,判定⑤正确.
试题解析:∵AB=AC,∠BAC=90°,点P是BC的中点,
∴∠EAP=![]() ∠BAC=45°,AP=
∠BAC=45°,AP=![]() BC=CP.
BC=CP.
①在△AEP与△CFP中,
∵∠EAP=∠C=45°,AP=CP,∠APE=∠CPF=90°-∠APF,
∴△AEP≌△CFP,
∴AE=CF.正确;
②由①知,△AEP≌△CFP,
∴∠APE=∠CPF.正确;
③由①知,△AEP≌△CFP,
∴PE=PF.
又∵∠EPF=90°,
∴△EPF是等腰直角三角形.正确;
④只有当F在AC中点时EF=AP,故不能得出EF=AP,错误;
⑤∵△AEP≌△CFP,同理可证△APF≌△BPE.
∴S四边形AEPF=S△AEP+S△APF=S△CPF+S△BPE=![]() S△ABC.正确.
S△ABC.正确.
故正确的序号有①②③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某保温杯专卖店通过市场调研,准备销售
 、
、 两种型号的保温杯,其中每件
两种型号的保温杯,其中每件 种保温杯的进价比
种保温杯的进价比 种保温杯的进价高20元,已知专卖店用3200元购进
种保温杯的进价高20元,已知专卖店用3200元购进 种保温杯的数量与用2560元购进
种保温杯的数量与用2560元购进 种保温杯的数量相同.
种保温杯的数量相同.(1)求两种保温杯的进价;
(2)若
 种保温杯的售价为250元,
种保温杯的售价为250元, 种保温杯的售价为180元,专卖店共进两种保温杯200个,设
种保温杯的售价为180元,专卖店共进两种保温杯200个,设 种保温杯进货
种保温杯进货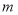 个,求该专卖店获得的总利润
个,求该专卖店获得的总利润 (元)与
(元)与 种保温杯进货数
种保温杯进货数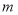 (个)之间的函数关系式,并写出自变量的取值范围.
(个)之间的函数关系式,并写出自变量的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)如图,平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,点P从O沿OB边向点B移动,点Q从点B沿BC边向点C移动,P,Q同时出发,速度都是1cm/s.
(1)求经过O,B,D三点的抛物线的解析式;
(2)判断P,Q移动几秒时,△PBQ为等腰三角形;
(3)若允许P点越过B点在BC上运动,Q点越过C点在CD上运动,设线PQ与OB,BC,DC围成的图形面积为y(cm2),点P,Q的移动时间为t(s),请写出y与t之间的函数关系式,并写出t的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,
 为坐标原点,矩形
为坐标原点,矩形 的顶点
的顶点 、
、 ,将矩形
,将矩形 的一个角沿直线
的一个角沿直线 折叠,使得点
折叠,使得点 落在对角线
落在对角线 上的点
上的点 处,折痕与
处,折痕与 轴交于点
轴交于点 .
.(1)求线段
 的长度;
的长度;(2)求直线
 所对应的函数表达式;
所对应的函数表达式;(3)若点
 在线段
在线段 上,在线段
上,在线段 上是否存在点
上是否存在点 ,使以
,使以 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期
一
二
三
四
五
六
日
增减/吨
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队承担了100米的道路改造工程任务,在确保工程质量的前提下,实际施工时每天改造道路比原计划多10米,结果提前5天完成了任务,求原计划平均每天改造道路多少米?
相关试题

