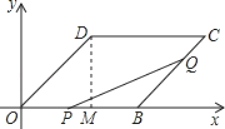
【题目】(本题满分12分)如图,平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,点P从O沿OB边向点B移动,点Q从点B沿BC边向点C移动,P,Q同时出发,速度都是1cm/s.
(1)求经过O,B,D三点的抛物线的解析式;
(2)判断P,Q移动几秒时,△PBQ为等腰三角形;
(3)若允许P点越过B点在BC上运动,Q点越过C点在CD上运动,设线PQ与OB,BC,DC围成的图形面积为y(cm2),点P,Q的移动时间为t(s),请写出y与t之间的函数关系式,并写出t的取值范围.

参考答案:
【答案】见解析
【解析】解:(1)过点D作DM⊥OB于M,
∵平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,
∴OD=BC=6cm,
∴OM=DM=ODsin45°=6×![]() =3
=3![]() ,
,
∴D(3![]() ,3
,3![]() ),B(8,0),
),B(8,0),
设经过O,B,D三点的抛物线的解析式为:y=ax(x﹣8),
将D的坐标代入得:3![]() =3
=3![]() a(3
a(3![]() ﹣8),
﹣8),
解得:a=﹣![]() ,∴y=﹣
,∴y=﹣![]() x(x﹣8);
x(x﹣8);
(2)∵∠PBQ=180°﹣∠DOB=135°,
∴若△PBQ为等腰三角形,则PB=BQ.
设P,Q移动t秒时,△PBQ为等腰三角形,
∴P点走过的路程为t,Q点走过的路程为t,
∴PB=OB﹣t=8﹣t(cm),BQ=tcm.若PB=BQ,则8﹣t=t,解得:t=4(s).
∴P,Q移动4秒时,△PBQ为等腰三角形;
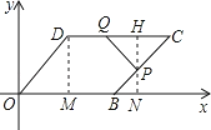
(3)如图:过点D作DM⊥OB于M,过点P作PN⊥OB于N,交CD于H,
∵四边形OBCD是平行四边形,
∴CD=OB=8cm,BC=OD=6cm,CD∥OB,HN=DM=3![]() cm,
cm,
∴PH⊥CD,△CPH∽△BPN,
∴![]() ,
,
由题意得:PC=14﹣t(cm),PB=t﹣8(cm),CQ=t﹣6(cm),
∴![]() ,
,
解得:PH=![]() (14﹣t),
(14﹣t),
∴y=SOBCD﹣S△CPQ=8×3![]() ﹣
﹣![]() (t﹣6)×
(t﹣6)×(14﹣t)=
![]() t2﹣5
t2﹣5![]() t+45
t+45![]() ,
,
∵P点越过B点在BC上运动,Q点越过C点在CD上运动,
∴8<t≤14,
∴y与t之间的函数关系式为y=![]() t2﹣5
t2﹣5![]() t+45
t+45![]() ,t的取值范围为8<t≤14.
,t的取值范围为8<t≤14.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,BD=DC,DE∥AB交AC于点E,BF⊥AC于F,交AD于P,PM⊥AB于M,下面五个结论中,正确的有__.(只填序号)
①PM=PF;②S△ABD=2S△DCE; ③四边形AMPF是正方形; ④∠BPD=∠BPM;⑤
 .
.
-
科目: 来源: 题型:
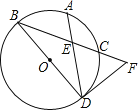
查看答案和解析>>【题目】(本题满分10分)如图,BD是⊙O的直径,点A是劣弧BC的中点,DF是⊙O的切线交BC于点F,AD交BC于点E.
(1)求证:EF=DF;
(2)若AE=2,ED=4,求EF的长.
-
科目: 来源: 题型:
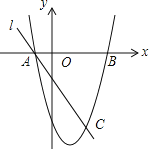
查看答案和解析>>【题目】(本题满分12分)如图,抛物线y=x2﹣2x﹣3与x轴交于A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B、C三点的坐标;
(2)在抛物线的对称轴上找到点P,使得△PBC的周长最小,并求出点P的坐标;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G为顶点四边形是平行四边形?如果存在,请直接写出F点坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程:
已知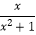 =
=  ,求
,求 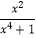 的值.
的值.
解:由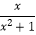 =
=  知x≠0,所以
知x≠0,所以 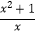 =3,即x+
=3,即x+ 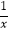 =3.所以
=3.所以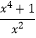 =x2+
=x2+ 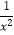 =
= 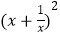 -2=32-2=7.
-2=32-2=7.
故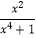 的值为
的值为  .
.
该题的解法叫做“倒数求值法”,请你利用“倒数求值法”解下面的题目:
若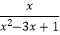 =
= 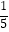 ,求
,求 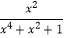 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面分别是三根小木棒的长度,能摆成三角形的是( )
A. 5cm,8cm,2cm B. 5cm,8cm,13cm
C. 5cm,8cm,5cm D. 2cm,7cm,5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各点中,在过点(-2,2)和(-2,4)的直线上的是( )
A.(-2,0)B.(-3,-3)C.(3,2)D.(5,4)
相关试题

