【题目】如图所示,二次函数y=ax2+bx+c(a ![]() 0)的图象,有下列4个结论:①abc>0;②b>a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的是 .
0)的图象,有下列4个结论:①abc>0;②b>a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的是 . 
参考答案:
【答案】③④
【解析】∵抛物线开口朝下,
∴a<0,
∵对称轴x=1=- ![]() ,
,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c>0,
∴abc<0,故①错误;
根据图象知道当x=-1时,y=a-b+c<0,
∴a+c<b,故②错误;
根据图象知道当x=2时,y=4a+2b+c>0,故③正确;
根据图象知道抛物线与x轴有两个交点,
∴b2-4ac>0,故④正确.
根据抛物线的开口方向向下得出a<0,根据抛物线的对称轴为直线x=1,得出- ![]() =1 ,从而得出b=-2a
=1 ,从而得出b=-2a![]() 0 ,再根据抛物线与y轴的交点在x轴的上方,得出c>0,进而得出abc<0 ;由图像知:当x=-1时,二次函数的图像在x轴的下方 ,故y=a-b+c<0 ,变形得a+c<b,根据图象知道当x=2时,二次函数的图像在x轴的上方 ,故y=4a+2b+c>0 ;根据图象知道抛物线与x轴有两个交点,故b2-4ac>0;从而就可以一一判断了。
0 ,再根据抛物线与y轴的交点在x轴的上方,得出c>0,进而得出abc<0 ;由图像知:当x=-1时,二次函数的图像在x轴的下方 ,故y=a-b+c<0 ,变形得a+c<b,根据图象知道当x=2时,二次函数的图像在x轴的上方 ,故y=4a+2b+c>0 ;根据图象知道抛物线与x轴有两个交点,故b2-4ac>0;从而就可以一一判断了。
-
科目: 来源: 题型:
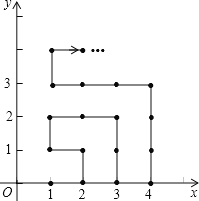
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→,…,根据这个规律,第2019个点的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为13,弦AB//CD,AB=24,CD=10,则AB、CD之间的距离为( )
A.17
B.7
C.12
D.7或17 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形 ABCD 中,E 为 BC 的中点,F 是 CD 上一点,且 CF
 CD ,
CD ,
求证:(1)∠AEF=90°;
(2) ∠BAE=∠EAF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小方格的边长 为 1,点 A、B、C 是格点.

(1)计算:AB= ;BC= ;AC= ;
(2)只用直尺(不带刻度)作出 AB 边上的高 CH(保留作图 痕迹)CH= ;
(3)只用直尺(不带刻度)作出 AC 边上的高 BG(保留作图痕迹).
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图 1,在 ABCD 中,AC、BD 交于点 O,过点 O 的直线 l 交 AB 于 E, 交 CD 于 F,①判断 OE 和 OF 的数量关系: ,并证明;
② S四边形AEFD S四边形CFEB (填“>” 或“=” 或“<”).
(2)如图 2 是一块“L”形的材料,请你作一条直线 m,使得直线 m 两边的材料的面积相等(保留作图痕迹,不用证明).
(3)如图 3,正方形 ABCD 的边长为 2
 cm,动点 P、Q 分别从点 A、C 同时出发,以 相同的速度分别沿 AD、CB 向终点 D、B 移动,当点 P 到达点 D 时,运动停止,过点 C 作 CH⊥PQ,垂足为点 H,连接 BH,则 BH 长的最小值为 cm(保留作图痕迹, 直接填写结果).
cm,动点 P、Q 分别从点 A、C 同时出发,以 相同的速度分别沿 AD、CB 向终点 D、B 移动,当点 P 到达点 D 时,运动停止,过点 C 作 CH⊥PQ,垂足为点 H,连接 BH,则 BH 长的最小值为 cm(保留作图痕迹, 直接填写结果).
相关试题

