【题目】（1）如图 1，在 ABCD 中，AC、BD 交于点 O，过点 O 的直线 l 交 AB 于 E， 交 CD 于 F，①判断 OE 和 OF 的数量关系： ，并证明；

② S四边形AEFD S四边形CFEB （填“>” 或“=” 或“<”）．

（2）如图 2 是一块“L”形的材料，请你作一条直线 m，使得直线 m 两边的材料的面积相等（保留作图痕迹，不用证明）．

（3）如图 3，正方形 ABCD 的边长为 2cm，动点 P、Q 分别从点 A、C 同时出发，以 相同的速度分别沿 AD、CB 向终点 D、B 移动，当点 P 到达点 D 时，运动停止，过点 C 作 CH⊥PQ，垂足为点 H，连接 BH，则 BH 长的最小值为 cm（保留作图痕迹， 直接填写结果）．

参考答案：

【答案】（1）①OE＝OF，证明见详解；②＝；（2）答案见详解；（3）

【解析】

（1）①通过证明△AOE≌△COF即可判断OE，OF的数量关系；

②利用平行四边形和全等三角形的性质得到，，然后利用等式的性质求解；

（2）直接利用矩形的性质结合中心对称图形的性质得出答案；

（3）设正方形的中心为O，可证PQ经过O点．连结OC，取OC中点M，连结 MH，MB，利用正方形的性质和勾股定理求出MB的长，利用直角三角形斜边中线等于斜边一半求出MH的长，然后利用两点之间线段最短解决问题即可．

解：（1）①∵四边形ABCD是平行四边形，

∴AO=OC，AB∥CD，

∴∠EAO=∠FCO，

在△EAO和△FCO中，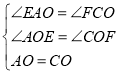

∴△AOE≌△COF

∴OE=OF

故答案为：OE=OF；

②∵在 ABCD 中，

又由①可知△AOE≌△COF

∴

∴

即S四边形AEFD=S四边形CFEB

故答案为：=；

（2）如图所示：

先找到两个矩形的中心，然后连接中心

直线m即为所求

（3）设正方形的中心为O，

由题意可知PD=BQ

∴在正方形ABCD中可知PQ经过O点．

连结OC，取OC中点M，连结 MH，MB，

∵正方形 ABCD 的边长为 2cm

∴CO=BO=，OM=MC=

∴

∵CH⊥PQ

∴MH=

BH≥BM-MH

即BH≥

∴当B，H，M三点共线时，BH最小为

故答案为：．

关闭