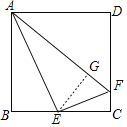
【题目】如图,在正方形 ABCD 中,E 为 BC 的中点,F 是 CD 上一点,且 CF ![]() CD ,
CD ,

求证:(1)∠AEF=90°;
(2) ∠BAE=∠EAF.
参考答案:
【答案】(1)证明见详解 (2)证明见详解
【解析】
(1)设正方形的边长为4a,先依据勾股定理求得AE、AF、EF的长,然后依据勾股定理的逆定理可证明结论;
(2)过点E作EG⊥AF于G,求出EG的长,得出BE=EG,则结论得证.
解:(1)证明:设AB=4a,
∵E为AB的中点,
∴BE=CE=2a,
∵CF=![]() CD,
CD,
∴CF=a,DF=3a,
∴AE=![]() a,EF=
a,EF=![]() a,AF=
a,AF=![]() =5a,
=5a,
∵AE2+EF2=(2![]() a)2+(
a)2+(![]() a)2=25a2,AF2=25a2,
a)2=25a2,AF2=25a2,
∴AE2+EF2=AF2
∴∠AEF=90°;
(2)过点E作EG⊥AF于G,
∵S△AEF=![]() ×2
×2![]() a×
a×![]() a=
a=![]() ×5a×EG,
×5a×EG,
∴EG=2a,
∴BE=EG,
又∵∠B=∠AGE=90°,
∴∠BAE=∠EAF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1 , 正八边形外侧八个扇形(有阴影部分)面积之和为S2 , 则
 =( )
=( )
A.
B.
C.
D.1 -
科目: 来源: 题型:
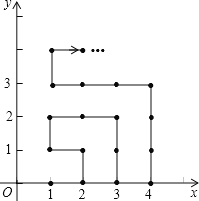
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)→,…,根据这个规律,第2019个点的坐标为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为13,弦AB//CD,AB=24,CD=10,则AB、CD之间的距离为( )
A.17
B.7
C.12
D.7或17 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,二次函数y=ax2+bx+c(a
 0)的图象,有下列4个结论:①abc>0;②b>a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的是 .
0)的图象,有下列4个结论:①abc>0;②b>a+c;③4a+2b+c>0;④b2-4ac>0;其中正确的是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小方格的边长 为 1,点 A、B、C 是格点.

(1)计算:AB= ;BC= ;AC= ;
(2)只用直尺(不带刻度)作出 AB 边上的高 CH(保留作图 痕迹)CH= ;
(3)只用直尺(不带刻度)作出 AC 边上的高 BG(保留作图痕迹).
相关试题

