Question

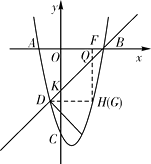
【题目】如图所示，已知抛物线经过点A（－2，0）、B（4，0）、C（0，－8），抛物线y＝ax2＋bx＋c（a≠0）与直线y＝x－4交于B ， D两点．

（1）求抛物线的解析式并直接写出D点的坐标；
（2）点P为抛物线上的一个动点，且在直线BD下方，试求出△BDP面积的最大值及此时点P的坐标；
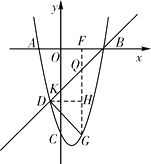
（3）点Q是线段BD上异于B、D的动点，过点Q作QF⊥x轴于点F ， 交抛物线于点G ． 当△QDG为直角三角形时，求点Q的坐标．

Answer 1

【答案】
（1）

设抛物线的解析式为y＝ax2＋bx＋c

∵抛物线经过点A（－2，0）、B（4，0）、C（0，－8）

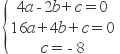∴ ,解得.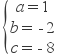

∴抛物线的解析式为y＝x2－2x－8

点D的坐标为（－1，－5）

（2）

过P作PE∥y轴，交直线AB于点E

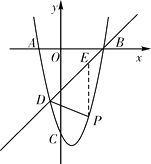
设P（x，x2－2x－8）则E（x，x－4）

∴PE＝x－4－(x2－2x－8)＝－x2＋3x＋4

∴S△BDP＝S△DEP＋S△BEP＝ PE·(xE－xD)＋ PE·(xB－xE)

＝ PE·(xB－xD)＝ PE＝ (－x2＋3x＋4)

＝－ (x－ )2＋

∴当x＝ 时，△BDP面积的最大值为

此时点P的坐标为（ ，－ ）

（3）

设直线y＝x－4与y轴相交于点K，则K（0，－4）

∵B（4，0），∴OB＝OK＝4，∴∠OKB＝∠OBK＝45°

∵QF⊥x轴，∴∠DQG＝45°

若△QDG为直角三角形，则△QDG是等腰直角三角形

①∠QDG＝90°，过D作DH⊥QG于H，∴QG＝2DH，

∴－x2＋3x＋4＝2(x＋1)，解得x 1＝－1（舍去），

x 2＝2，∴Q1（2，－2）

②∠DGQ＝90°，则DH＝QH，

∴－x2＋3x＋4＝x+1，解得x 1＝-1（舍去），x 2＝3，∴P2（3，－1）

综上所述，当△QDG为直角三角形时，点Q的坐标为（2，－2）或（3，－1）

【解析】（1）设出一元二次函数，利用待定系数法求出a、b、c的值；
（2）设出PE两点的坐标，从图中可以看出SBDP=SEPB+SEPD.运用二次函数的性质求出SBDP的的最值及P点的坐标；
（3）一次函数为y=x-4，则意味着∠OKB=∠OBK=45°，则如果△QDG是直角三角形，必定是等腰直角三角形。但接下来要分两种情况去进行讨论：①∠QDG=90°；②∠DGQ=90°.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识，掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点，以及对二次函数的性质的理解，了解增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．