【题目】如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E. 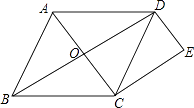
(1)求证:四边形CODE是矩形;
(2)若AB=5,AC=6,求四边形CODE的周长.
参考答案:
【答案】
(1)证明:如图,∵四边形ABCD为菱形,
∴∠COD=90°;而CE∥BD,DE∥AC,
∴∠OCE=∠ODE=90°,
∴四边形CODE是矩形
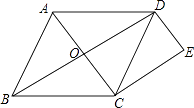
(2)解:∵四边形ABCD为菱形,
∴AO=OC= ![]() AC=3,OD=OB,∠AOB=90°,
AC=3,OD=OB,∠AOB=90°,
由勾股定理得:
BO2=AB2﹣AO2,而AB=5,
∴DO=BO=4,
∴四边形CODE的周长=2(3+4)=14
【解析】(1)如图,首先证明∠COD=90°;然后证明∠OCE=∠ODE=90°,即可解决问题.(2)如图,首先证明CO=AO=3,∠AOB=90°;运用勾股定理求出BO,即可解决问题.
【考点精析】根据题目的已知条件,利用菱形的性质和矩形的判定方法的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.
-
科目: 来源: 题型:
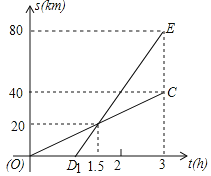
查看答案和解析>>【题目】已知A、B两地相距80km,甲、乙两人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DE、OC分别表示甲、乙两人离开A地的距离(km)与乙出发的时间(h)的关系,根据图象填空:
(1)乙先出发__h后,甲才出发;
(2)大约在乙出发后__h,两人相遇,这时他们离A地__km;
(3)甲到达B地时,乙离开A地__km;
(4)甲的速度是__km/h;乙的速度是__km/h;
(5)甲离开A地的距离s(km)与乙出发的时间t(h)的关系式为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在解决问题:已知a=
 ,求2a2﹣8a+1的值,他是这样分析与解的:
,求2a2﹣8a+1的值,他是这样分析与解的:∵a=
 =
= =2﹣
=2﹣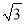
∴a﹣2=﹣

∴(a﹣2)2=3,a2﹣4a+4=3
∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1
请你根据小明的分析过程,解决如下问题:
(1)化简
 +
+ +
+ +…+
+…+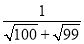
(2)若a=
 ,求4a2﹣8a+1的值.
,求4a2﹣8a+1的值. -
科目: 来源: 题型:
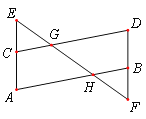
查看答案和解析>>【题目】已知:如图,∠A=∠D,∠EGC=∠FHB
(1)求证:AB∥CD
(2)求证:∠E=∠F
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的顶点A是双曲线y1=
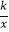 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=  .
. 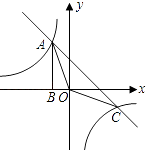
(1)求这两个函数的解析式;
(2)求△AOC的面积;
(3)直接写出使y1>y2成立的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数的图象经过点(﹣2,﹣2)和点(2,4).
(1)求这个函数的解析式;
(2)判断点P(1,1)是否在此函数图象上,并说明理由.
(3)求这个函数的图象与坐标轴围成的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山西省)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

相关试题

