【题目】小明在解决问题:已知a=![]() ,求2a2﹣8a+1的值,他是这样分析与解的:
,求2a2﹣8a+1的值,他是这样分析与解的:
∵a=![]() =
= =2﹣
=2﹣![]()
∴a﹣2=﹣![]()
∴(a﹣2)2=3,a2﹣4a+4=3
∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1
请你根据小明的分析过程,解决如下问题:
(1)化简![]() +
+![]() +
+![]() +…+
+…+![]()
(2)若a=![]() ,求4a2﹣8a+1的值.
,求4a2﹣8a+1的值.
参考答案:
【答案】(1)9;(2)5.
【解析】试题分析:
(1)此式必须在把分母有理化后才能实现化简,即各分式分子分母同乘以一个因式,使得与分母相乘后,为平方差公式结构,如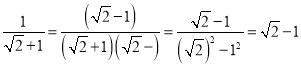 .
.
(2)先对a值进行化简得![]() ,若就接着代入求解,计算量偏大。模仿小明做法,可先计算
,若就接着代入求解,计算量偏大。模仿小明做法,可先计算![]() 的值,就能较为简单地算出结果;也可对这个二次三项式进行配方,再代入求值。后两种方法都比直接代入计算量小很多.
的值,就能较为简单地算出结果;也可对这个二次三项式进行配方,再代入求值。后两种方法都比直接代入计算量小很多.
解:(1)原式=![]()
![]()
(2)∵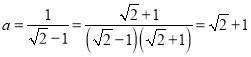 ,
,
解法一:∵![]() ,
,
∴![]() ,即
,即![]()
∴原式=![]()
解法二∴ 原式=![]()
![]()
![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班组织去方特参加秋季社会实践活动,其中第一小组有x人,第二小组的人数比第一小组人数的
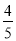 少30人,如果从第二小组调出10人到第一小组,那么:
少30人,如果从第二小组调出10人到第一小组,那么:(1)两个小组共有多少人?
(2)调动后,第一小组的人数比第二小组多多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,阳光下,小亮的身高如图中线段AB所示,他在地面上的影子如图中线段BC所示,线段DE表示旗杆的高,线段FG表示一堵高墙.
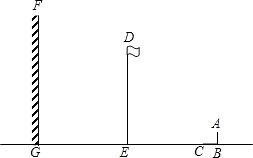
(1)请你在图中画出旗杆在同一时刻阳光照射下形成的影子;
(2)如果小亮的身高AB=1.6m,他的影子BC=2.4m,旗杆的高DE=15m,旗杆与高墙的距离EG=16m,请求出旗杆的影子落在墙上的长度. -
科目: 来源: 题型:
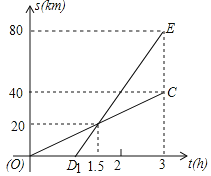
查看答案和解析>>【题目】已知A、B两地相距80km,甲、乙两人沿同一条公路从A地到B地,乙骑自行车,甲骑摩托车,DE、OC分别表示甲、乙两人离开A地的距离(km)与乙出发的时间(h)的关系,根据图象填空:
(1)乙先出发__h后,甲才出发;
(2)大约在乙出发后__h,两人相遇,这时他们离A地__km;
(3)甲到达B地时,乙离开A地__km;
(4)甲的速度是__km/h;乙的速度是__km/h;
(5)甲离开A地的距离s(km)与乙出发的时间t(h)的关系式为_____.
-
科目: 来源: 题型:
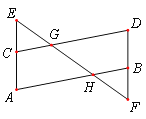
查看答案和解析>>【题目】已知:如图,∠A=∠D,∠EGC=∠FHB
(1)求证:AB∥CD
(2)求证:∠E=∠F
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
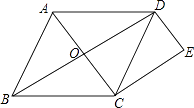
(1)求证:四边形CODE是矩形;
(2)若AB=5,AC=6,求四边形CODE的周长. -
科目: 来源: 题型:
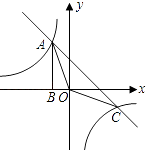
查看答案和解析>>【题目】如图,Rt△ABO的顶点A是双曲线y1=
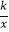 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=  .
. 
(1)求这两个函数的解析式;
(2)求△AOC的面积;
(3)直接写出使y1>y2成立的x的取值范围.
相关试题

