【题目】已知一次函数的图象经过点(﹣2,﹣2)和点(2,4).
(1)求这个函数的解析式;
(2)判断点P(1,1)是否在此函数图象上,并说明理由.
(3)求这个函数的图象与坐标轴围成的面积.
参考答案:
【答案】(1)y=![]() x+1;(2)点 P(1,1)不在此函数图象上;(3)
x+1;(2)点 P(1,1)不在此函数图象上;(3)![]() .
.
【解析】试题分析:(1)使用待定系数法求解析式,设解析式为y=kx+b,然后代入图像中的已知点,得到两个关于k,b的方程,解方程组,问题得解.
(2)把点p代入解析式左右两边,若相等,说明是在图像上,否则不在.
(3)首先要找到与坐标轴的交点,做出图像,找出与坐标轴围城的图形,就可以求面积.其中与y轴交点为(0,b),通过令y=0,得kx+b=0,解方程求出x,即可得到与x轴交点.
解:(1)设一次函数解析式为y=kx+b(k≠0),
将(﹣2,﹣2)、(2,4)代入y=kx+b中,
![]() , 解得:
, 解得: 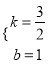 ,
,
∴这个函数的解析式为![]()
(2)当x=1时, ![]()
∴点 P(1,1)不在此函数图象上.
(3)当x=0时,y=1,
∴该函数图象与y轴交点坐标为(0,1);
当y=0时,有![]() ,解得:
,解得: ![]() ,
,
∴该函数图象与x轴交点坐标为![]() 如图所示,
如图所示,
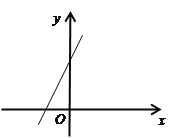
∴这个函数的图象与坐标轴围成的面积![]() .
.
-
科目: 来源: 题型:
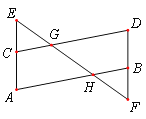
查看答案和解析>>【题目】已知:如图,∠A=∠D,∠EGC=∠FHB
(1)求证:AB∥CD
(2)求证:∠E=∠F
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
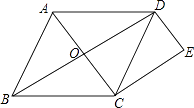
(1)求证:四边形CODE是矩形;
(2)若AB=5,AC=6,求四边形CODE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABO的顶点A是双曲线y1=
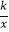 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=  .
. 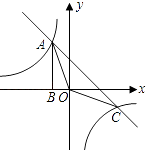
(1)求这两个函数的解析式;
(2)求△AOC的面积;
(3)直接写出使y1>y2成立的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2016山西省)我省某苹果基地销售优质苹果,该基地对需要送货且购买量在2000kg﹣5000kg(含2000kg和5000kg)的客户有两种销售方案(客户只能选择其中一种方案):
方案A:每千克5.8元,由基地免费送货.
方案B:每千克5元,客户需支付运费2000元.
(1)请分别写出按方案A,方案B购买这种苹果的应付款y(元)与购买量x(kg)之间的函数表达式;
(2)求购买量x在什么范围时,选用方案A比方案B付款少;
(3)某水果批发商计划用20000元,选用这两种方案中的一种,购买尽可能多的这种苹果,请直接写出他应选择哪种方案.

-
科目: 来源: 题型:
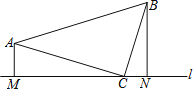
查看答案和解析>>【题目】如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线
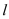 的垂线,垂足分别为M、N.
的垂线,垂足分别为M、N.(1)求证:△AMC≌△CNB;
(2)若AM=3,BN=5,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形ABCD是平行四边形,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.
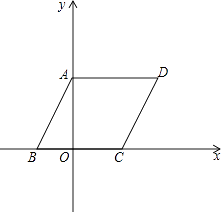
(1)求OA、OB的长.
(2)若点E为x轴正半轴上的点,且S△AOE=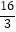 ,求经过D、E两点的直线解析式及经过点D的反比例函数的解析式,并判断△AOE与△AOD是否相似.
,求经过D、E两点的直线解析式及经过点D的反比例函数的解析式,并判断△AOE与△AOD是否相似.
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,直接写出F点的坐标,若不存在,请说明理由.
相关试题

