【题目】二次函数y=ax2﹣bx+b(a>0,b>0)图象的顶点的纵坐标不大于 ![]() ,且图象与x轴交于A,B两点,则线段AB长度的最小值是 .
,且图象与x轴交于A,B两点,则线段AB长度的最小值是 .
参考答案:
【答案】2 ![]()
【解析】解:∵抛物线顶点横坐标为x=﹣ ![]() =
= ![]() ,
,
代入得:y=a ![]() ﹣
﹣ ![]() =b≤﹣
=b≤﹣ ![]() ,
,
化简得: ![]() ≥3,即b≥6a,(此时△>0,符合题意)
≥3,即b≥6a,(此时△>0,符合题意)
∵当y=ax2﹣bx+b=0,时,x1= ![]() ,x2=
,x2= ![]() ,
,
∴AB= ![]() ,
,
∵a、b均大于0,
∴当b=6a时,AB有最小值为2 ![]() ,
,
所以答案是 2 ![]() .
.
【考点精析】掌握二次函数的性质和二次函数的最值是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已如两个全等的等腰△ABC、△DEF,其中∠ACB=∠DFE=90°,E为AB中点,△DEF可绕顶点E旋转,线段DE,EF分别交线段CA,CB(或它们所在的直线)于M、N.
(1)如图1,当线段EF经过△ABC的顶点时,点N与点C重合,线段DE交AC于M,已知AC=BC=5,则MC= ;
(2)如果2,当线段EF与线段BC边交于N点,线段DE与线段AC交于M点,连MN,EC,请探究AM,MN,CN之间的等量关系,并说明理由;
(3)如图3,当线段EF与BC延长线交于N点,线段DE与线段AC交于M点,连MN,EC,则(2)中AM,MN,CN之间的等量关系还成立吗?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD 中,对角线 AC 与 BD 相交于点 O ,点 E , F 分别为 OB , OD 的中点,延长 AE 至 G ,使 EG =AE ,连接 CG .
(1)求证: △ABE≌△CDF ;
(2)当 AB 与 AC 满足什么数量关系时,四边形 EGCF 是矩形?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ,
 =
=  =
=  =n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ= , n= .
=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ= , n= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:二次根式与分式运算
(1)计算:( )﹣2+(
)﹣2+(  ﹣
﹣  )0+(﹣1)1001+(
)0+(﹣1)1001+(  ﹣3
﹣3  )×tan30°
)×tan30°
(2)先化简,再求值: ﹣
﹣  (
(  ﹣a2+b2),其中a=3﹣2
﹣a2+b2),其中a=3﹣2  ,b=3
,b=3  ﹣3.
﹣3. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知
 ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”
 ,必有实数根;
,必有实数根;(3)若 x 1是“勾系一元二次方程”
 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6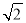 ,求ABC 的面积.
,求ABC 的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展,体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题:

(1)求扇形统计图中m的值,并补全条形统计图;
(2)在被调查的学生中,随机抽一人,抽到选“体育特长类”或“艺术特长类”的学生的概率是多少?
(3)已知该校有800名学生,计划开设“实践活动类”课程每班安排20人,问学校开设多少个“实践活动类”课程的班级比较合理?
相关试题

