【题目】已知:![]() 、
、![]() 两地相距
两地相距![]() ,甲、乙两车分别从
,甲、乙两车分别从![]() 、
、![]() 两地同时出发,甲速每小时
两地同时出发,甲速每小时![]() 千米,乙速每小时
千米,乙速每小时![]() 千米,请按下列要求列方程解题:
千米,请按下列要求列方程解题:
![]() 若同时出发,相向而行,多少小时相遇?
若同时出发,相向而行,多少小时相遇?
![]() 若同时出发,相向而行,多长时间后两车相距
若同时出发,相向而行,多长时间后两车相距![]() ?
?
![]() 若同时出发,同向而行,多长时间后两车相距
若同时出发,同向而行,多长时间后两车相距![]() ?
?
参考答案:
【答案】(1) 同时出发,相向而行,![]() 小时相遇;(2) 同时出发,相向而行,
小时相遇;(2) 同时出发,相向而行,![]() 小时或
小时或![]() 小时后两车相距
小时后两车相距![]() ;(3) 两车同时出发,同向而行,
;(3) 两车同时出发,同向而行,![]() 小时或
小时或![]() 小时后两车相距
小时后两车相距![]() .
.
【解析】
(1)若同时出发,相向而行,设x小时相遇,根据两车行驶的路程之和是500km列出方程并解答;
(2)设两车同时出发,相向而行,y小时后两车相距100km,此题要分两种情况:①相遇前,甲乙两车路程=500-100=400,②相遇后甲乙两车路程=500+100=600,根据等量关系列出方程,再解即可;
(3)设两车同时出发,同向而行,z小时后两车相距100km,此题属于追及问题,要分两种情况:①追上前相差100km,甲乙两车路程差=500-100=400,②追上之后并超过100km,甲乙两车路程差=500+100=600,根据等量关系列出方程,再解即可.
(1)若同时出发,相向而行,![]() 小时相遇;
小时相遇;
![]() 设两车同时出发,相向而行,
设两车同时出发,相向而行,![]() 小时后两车相距
小时后两车相距![]() ,
,
①相遇前,两车相距![]() ,
,
依题意得:![]() ,
,
解得![]() ;
;
②相遇后,两车相距![]() ,
,
依题意得:![]() ,
,
解得![]() ;
;
综上所述,若同时出发,相向而行,![]() 小时或
小时或![]() 小时后两车相距
小时后两车相距![]() .
.
答:若同时出发,相向而行,![]() 小时或
小时或![]() 小时后两车相距
小时后两车相距![]() .
.
![]() 设两车同时出发,同向而行,
设两车同时出发,同向而行,![]() 小时后两车相距
小时后两车相距![]() ,
,
①相遇前:![]() ,
,
解得:![]() ,
,
②相遇后:![]() ,
,
解得:![]() .
.
答:两车同时出发,同向而行,![]() 小时或
小时或![]() 小时后两车相距
小时后两车相距![]() .
.
故答案为:(1) 同时出发,相向而行,![]() 小时相遇;(2) 同时出发,相向而行,
小时相遇;(2) 同时出发,相向而行,![]() 小时或
小时或![]() 小时后两车相距
小时后两车相距![]() ;(3) 两车同时出发,同向而行,
;(3) 两车同时出发,同向而行,![]() 小时或
小时或![]() 小时后两车相距
小时后两车相距![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(2k﹣3)x+k2+1=0有两个不相等的实数根x1、x2 .
(1)求k的取值范围;
(2)试说明x1<0,x2<0;
(3)若抛物线y=x2﹣(2k﹣3)x+k2+1与x轴交于A、B两点,点A、点B到原点的距离分别为OA、OB,且OA+OB=2OAOB﹣3,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解答问题.
材料:将一组正整数1,2,3,4,5,…按下面的方法进行排列:

我们规定:正整数2的位置记为(1,2),正整数8的位置记为(2,5).
问题:(1)若一个数a的位置记作(4,3),则a=________;
(2)正整数2017的位置可记为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
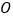 为直线
为直线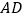 上一点,以
上一点,以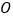 为顶点作
为顶点作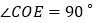 ,射线
,射线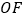 平分
平分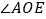 .
.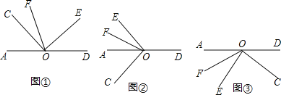
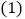 如图①,
如图①,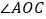 与
与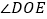 的数量关系为________,
的数量关系为________,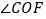 和
和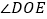 的数量关系为_________;
的数量关系为_________;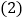 若将
若将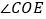 绕点
绕点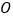 旋转至图②的位置,
旋转至图②的位置,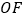 依然平分
依然平分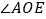 ,请写出
,请写出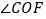 和
和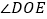 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;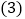 若将
若将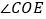 绕点
绕点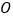 旋转至图③的位置,射线
旋转至图③的位置,射线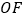 依然平分
依然平分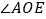 ,请直接写出
,请直接写出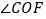 和
和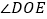 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知点A(4-a,-2a-3)和点B(-2,5),且AB∥x轴,试求点A的坐标;
(2)把点P(m+1,n-2m)先向右平移4个单位长度,再向下平移6个单位长度后得到点P′的坐标为(3,-2),试求m,n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y=(3-2m)x+m-1是y关于x的一次函数.
(1)若y随着x的增大而减小,求m的取值范围;
(2)若函数的图象与直线y=-3x平行,试确定该函数的表达式;
(3)若函数的图象经过点(-1,5m+2),试确定该函数的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[k-1,k2-1]的一次函数为正比例函数,求k的值;
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且△OAB的面积为4(O为原点),若一次函数的图象过A,B两点,求该一次函数的特征数.
相关试题

