【题目】已知y=(3-2m)x+m-1是y关于x的一次函数.
(1)若y随着x的增大而减小,求m的取值范围;
(2)若函数的图象与直线y=-3x平行,试确定该函数的表达式;
(3)若函数的图象经过点(-1,5m+2),试确定该函数的表达式.
参考答案:
【答案】(1) m>![]() ;(2) y=-3x+2;(3) y=9x-4.
;(2) y=-3x+2;(3) y=9x-4.
【解析】(1)由y随x的增大而减小知k<0,据此列出关于m的不等式,解之可得;
(2)由两直线平行时知斜率相等,得出关于m的方程,解之得出m的值即可得;
(3)将点(﹣1,5m+2)代入直线解析式可得m的值,据此可得.
(1)根据题意知,3﹣2m<0,解得:m>![]() ;
;
(2)根据题意,得:3﹣2m=﹣3,解得:m=3,则所求函数解析式为y=﹣3x+2;
(3)将(﹣1,5m+2)代入y=(3﹣2m)x+m﹣1,得:﹣(3﹣2m)+m﹣1=5m+2,解得:m=﹣3,则所求函数解析式为y=9x﹣4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
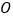 为直线
为直线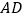 上一点,以
上一点,以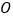 为顶点作
为顶点作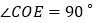 ,射线
,射线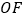 平分
平分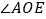 .
.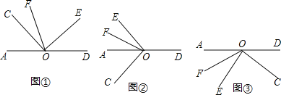
 如图①,
如图①,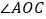 与
与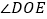 的数量关系为________,
的数量关系为________,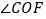 和
和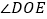 的数量关系为_________;
的数量关系为_________;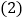 若将
若将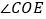 绕点
绕点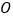 旋转至图②的位置,
旋转至图②的位置,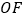 依然平分
依然平分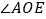 ,请写出
,请写出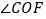 和
和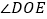 之间的数量关系,并说明理由;
之间的数量关系,并说明理由; 若将
若将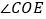 绕点
绕点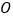 旋转至图③的位置,射线
旋转至图③的位置,射线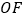 依然平分
依然平分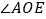 ,请直接写出
,请直接写出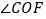 和
和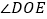 之间的数量关系.
之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 、
、 两地相距
两地相距 ,甲、乙两车分别从
,甲、乙两车分别从 、
、 两地同时出发,甲速每小时
两地同时出发,甲速每小时 千米,乙速每小时
千米,乙速每小时 千米,请按下列要求列方程解题:
千米,请按下列要求列方程解题: 若同时出发,相向而行,多少小时相遇?
若同时出发,相向而行,多少小时相遇? 若同时出发,相向而行,多长时间后两车相距
若同时出发,相向而行,多长时间后两车相距 ?
? 若同时出发,同向而行,多长时间后两车相距
若同时出发,同向而行,多长时间后两车相距 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知点A(4-a,-2a-3)和点B(-2,5),且AB∥x轴,试求点A的坐标;
(2)把点P(m+1,n-2m)先向右平移4个单位长度,再向下平移6个单位长度后得到点P′的坐标为(3,-2),试求m,n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义[p,q]为一次函数y=px+q的特征数.
(1)若特征数是[k-1,k2-1]的一次函数为正比例函数,求k的值;
(2)在平面直角坐标系中,有两点A(-m,0),B(0,-2m),且△OAB的面积为4(O为原点),若一次函数的图象过A,B两点,求该一次函数的特征数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式:①
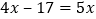 ;②
;②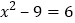 ;③
;③ ;④
;④ ;⑤
;⑤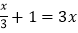 ;⑥
;⑥ ;⑦
;⑦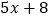 ;⑧
;⑧ 中方程有________,一元一次方程有________(只填序号).
中方程有________,一元一次方程有________(只填序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】移动公司推出两种话费套餐,套餐一:每月收取月租34元后,送50分钟的通话时间,超过50分钟的部分每分钟收费0.2元,并约定每月最低消费40元(当月通话费用不足40元,一律按40元收取);套餐二:每月没有最低消费,但每分钟均收取0.4元的通话费用.若分别用y1,y2(单位:元)表示套餐一、套餐二的通话费用,用x(单位:分钟)表示每个月的通话时间.
(1)分别求出y1,y2关于x的函数表达式;
(2)在如图所示的平面直角坐标系中,画出这两个函数的图象,并直接写出这两个函数图象的交点坐标;
(3)①结合图象,如何选择话费套餐才可使每月支付的通话费用较少?
②若小亮的爸爸这个月的通话费用是64元,求使用两种套餐的通话时间相差多少分钟.

相关试题

