【题目】在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.
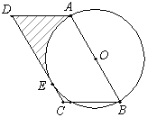
(1)圆心O到CD的距离是______;
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)
参考答案:
【答案】(1)、5;(2)、25+![]() -
-![]() .
.
【解析】
试题分析:(1)、连接OE,根据切线可得OE⊥CD,根据AB求出OE的长度,即圆心到CD的距离;(2)、根据平行四边形得出∠C=120°,∠BOE=90°,作EF∥CB,根据Rt△OEF求出OF的长度,然后得出EC和DE长度,从而求出梯形OADE的面积和扇形OAE的面积,从而得出阴影部分的面积.
试题解析:(1)、连接OE.
∵边CD切⊙O于点E.∴OE⊥CD 则OE就是圆心O到CD的距离,则圆心O到CD的距离是![]() ×AB=5.
×AB=5.
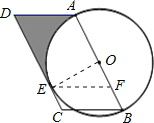
(2)∵四边形ABCD是平行四边形. ∴∠C=∠DAB=180°-∠ABC=120°,
∴∠BOE=360°-90°-60°-120°=90°, ∴∠AOE=90°,
作EF∥CB,∴∠OFE=∠ABC=60°, 在直角三角形OEF中,OE=5,
∴OF=OE![]() tan30°=
tan30°=![]() .EC=BF=5-
.EC=BF=5-![]() . 则DE=10-5+
. 则DE=10-5+![]() =5+
=5+![]() ,
,
则直角梯形OADE的面积是:![]() (OA+DE)×OE=
(OA+DE)×OE=![]() (5+5+
(5+5+![]() )×5=25+
)×5=25+![]() .
.
扇形OAE的面积是:![]() . 则阴影部分的面积是:25+
. 则阴影部分的面积是:25+![]() -
-![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的面积;
(2)当t为几秒时,BP平分∠ABC;
(3)问t为何值时,△BCP为等腰三角形?
(4)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒2cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分?

-
科目: 来源: 题型:
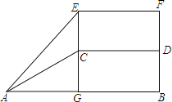
查看答案和解析>>【题目】如图是扬州某商场的自动扶梯侧面示意图,已知自动扶梯AC的坡度为1:2,AC的长度为5
 米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.(参考数据:sin42°=
米,AB为底楼地面,CD为二楼侧面,EF为二楼楼顶,当然有EF∥AB∥CD,E为自动扶梯AC的最高端C的正上方,过C的直线EG⊥AB于G,在自动扶梯的底端A测得E的仰角为42°,求该商场二楼的楼高CE.(参考数据:sin42°=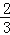 ,cos42°=
,cos42°= ,tan42°=
,tan42°=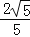 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“到一个角的两边距离相等的点,在这个角的平分线上”它的逆命题是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a,b,c是实数,点A(a+1,b),B(a+2,c)在二次函数y=x2-2ax+3的图象上,则b,c的大小关系是b_____c.(用“>”或“<”填空)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.

相关试题

