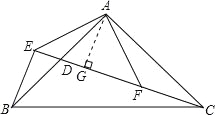
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.

参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、通过证△AEB≌△AFC(SAS),得到AE=AF;(2)、如图,过点A作AG⊥EC,垂足为G,通过证△BED≌△AGD(AAS),得到ED=GD,BE=AG,易证CF=BE=AG=GF.因为CD=DG+GF+FC,所以CD=DE+BE+BE,故CD=2BE+DE.
试题解析:(1)、如图,∵∠BAC=90°,AF⊥AE, ∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC, ∵BE⊥CD, ∴∠BEC=90°, ∴∠EBD+∠EDB=∠ADC+∠ACD=90°,
∵∠EDB=∠ADC, ∴∠EBA=∠ACF, ∴在△AEB与△AFC中, ,
,
∴△AEB≌△AFC(ASA), ∴AE=AF;
(2)、如图,过点A作AG⊥EC,垂足为G. ∵AG⊥EC,BE⊥CE, ∴∠BED=∠AGD=90°,
∵点D是AB的中点, ∴BD=AD. ∴在△BED与△AGD中,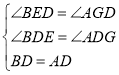 , ∴△BED≌△AGD(AAS), ∴ED=GD,BE=AG, ∵AE=AF ∴∠AEF=∠AFE=45° ∴∠FAG=45° ∴∠GAF=∠GFA, ∴GA=GF, ∴CF=BE=AG=GF, ∵CD=DG+GF+FC, ∴CD=DE+BE+BE, ∴CD=2BE+DE.
, ∴△BED≌△AGD(AAS), ∴ED=GD,BE=AG, ∵AE=AF ∴∠AEF=∠AFE=45° ∴∠FAG=45° ∴∠GAF=∠GFA, ∴GA=GF, ∴CF=BE=AG=GF, ∵CD=DG+GF+FC, ∴CD=DE+BE+BE, ∴CD=2BE+DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.
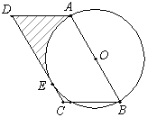
(1)圆心O到CD的距离是______;
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积.(结果保留π和根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“到一个角的两边距离相等的点,在这个角的平分线上”它的逆命题是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】a,b,c是实数,点A(a+1,b),B(a+2,c)在二次函数y=x2-2ax+3的图象上,则b,c的大小关系是b_____c.(用“>”或“<”填空)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列逆命题是真命题的是( )
A.如果x=y,那么x2=y2
B.相等的角是内错角
C.有三个角是60°的三角形是等边三角形
D.全等三角形的对应角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(1)﹣3m+2m﹣5m;(2)(2a2﹣1+2a)﹣(a﹣1+a2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学计划购买A型和B型课桌凳共200套. 经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1820元.(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)、学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的
 ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
相关试题

