搜索
【题目】“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70km/h．如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处，过了2s后，测得小汽车与车速检测仪间距离为50m，这辆小汽车超速了吗？（参考数据转换：1m/s=3.6km/h）
参考答案：
【答案】超速；理由见解析
【解析】
试题分析：本题求小汽车是否超速，其实就是求BC的距离，直角三角形ABC中，有斜边AB的长，有直角边AC的长，那么BC的长就很容易求得，根据小汽车用2s行驶的路程为BC，那么可求出小汽车的速度，然后再判断是否超速了．
试题解析：在Rt△ABC中，AC=30m，AB=50m； 据勾股定理可得：
（m）
∴小汽车的速度为v=
=20（m/s）=20×3.6（km/h）=72（km/h）； ∵72（km/h）＞70（km/h）；
∴这辆小汽车超速行驶．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各组数中，能成为直角三角形的三条边长的是（ ）
A.8、15、17
B.10、24、25
C.9、15、20
D.9、80、81 -
科目： 来源： 题型：
查看答案和解析>>【题目】下列调查中，调查方式选择正确的是( )
A. 为了了解1 000个灯泡的使用寿命，选择全面调查
B. 为了了解某公园全年的游客流量， 选择抽样调查
C. 为了了解生产的一批炮弹的杀伤半径，选择全面调查
D. 为了了解一批袋装食品是否含有防腐剂，选择全面调查
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠ACB=90°，BD是∠ABC的平分线，点O在AB上，⊙O经过B，D两点，交BC于点E．
（1）求证：AC是⊙O的切线；
（2）若AB=6，sin∠BAC=
，求BE的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠C=90°，AB=10cm，BC=6cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．
（1）出发2秒后，求△ABP的面积；
（2）当t为几秒时，BP平分∠ABC；
（3）问t为何值时，△BCP为等腰三角形？
（4）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？
-
科目： 来源： 题型：
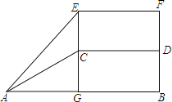
查看答案和解析>>【题目】如图是扬州某商场的自动扶梯侧面示意图，已知自动扶梯AC的坡度为1：2，AC的长度为5
米，AB为底楼地面，CD为二楼侧面，EF为二楼楼顶，当然有EF∥AB∥CD，E为自动扶梯AC的最高端C的正上方，过C的直线EG⊥AB于G，在自动扶梯的底端A测得E的仰角为42°，求该商场二楼的楼高CE．（参考数据：sin42°=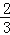
，cos42°=
，tan42°=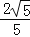
）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平行四边形ABCD中，AB=10，∠ABC=60°，以AB为直径作⊙O，边CD切⊙O于点E．
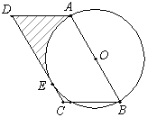
(1)圆心O到CD的距离是______；
(2)求由弧AE、线段AD、DE所围成的阴影部分的面积．（结果保留π和根号）
相关试题
