搜索
【题目】如图，二次函数y=ax2+bx+c图象对称轴是直线x=1，则下列结论：
①a＜0，b＜0，
②2a﹣b＞0，
③a+b+c＞0，
④a﹣b+c＜0，
⑤当x＞1时，y随x的增大而减小，
其中正确的是（ ）
A.①②③
B.②③④
C.③④⑤
D.①③④
参考答案：
【答案】C
【解析】解：①∵抛物线开口向下，
∴a＜0，
∵抛物线的对称轴为x=﹣ 
=1，
∴b=﹣2a＞0，①错误；
②∵b=﹣2a，a＜0，
∴2a﹣b=2a﹣（﹣2a）=4a＜0，②错误；
③根据函数图象可知：当x=1时，y＞0，
∴a+b+c＞0，③正确；
④根据函数图象可知：当x=﹣1时，y＜0，
∴a﹣b+c＜0，④正确；
⑤根据函数图象可知：当x＞1时，y随x的增大而减小，⑤正确．
综上可知：正确的结论有③④⑤．
故选C．
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系，掌握二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：3+2
=（1+
）2，善于思考的小明进行了以下探索：
设a+b
=（m+n
）2（其中a、b、m、n均为整数），则有a+b
=m2+2n2+2mn
，∴a=m2+2n2，b=2mn，这样小明就找到了一种把部分a+b
的式子化为平方式的方法。
请我仿照小明的方法探索并解决下列问题：
（1）当a、b、m、n均为正整数时，若a+b
=（m+n
）2，用含m、n的式子分别表示a、b，得a=________, b=___________.（2）若a+4
=（m+n
）2，且a、m、n均为正整数，求a的值。 -
科目： 来源： 题型：
查看答案和解析>>【题目】某体育用品商店购进一批滑板，每件进价为100元，售价为130元，每星期可卖出80件．商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20件．
（1）求商家降价前每星期的销售利润为多少元？
（2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系内，一次函数y=ax+b与二次函数y=ax2+2x+b的图象可能是（ ）
A.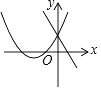
B.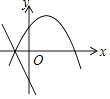
C.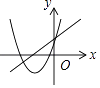
D.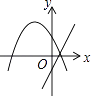
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系内，一次函数y=ax+b与二次函数y=ax2+2x+b的图象可能是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】数轴上点
对应的数为
，点
对应的数为
，点
为数轴上一动点.（1） AB的距离是 ．
（2） ①若点
到点的距离比到点的距离大1，点对应的数为 ．②若点
其对应的数为
，数轴上是否存在点，使点到点，点的距离之和为8？若存在，请求出的值；若不存在，请说明理由．（3）当点
以每秒钟
个单位长度从原点
向右运动时，点
以每秒钟
个单位长度的速度从点向左运动，点
以每秒钟
个单位长度的速度从点向右运动，问它们同时出发 秒钟时，
（直接写出答案即可）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=ax2+bx+c图象对称轴是直线x=1，则下列结论：
①a＜0，b＜0，
②2a﹣b＞0，
③a+b+c＞0，
④a﹣b+c＜0，
⑤当x＞1时，y随x的增大而减小，
其中正确的是（ ）
A.①②③
B.②③④
C.③④⑤
D.①③④
相关试题
