【题目】数轴上点![]() 对应的数为
对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,点
,点![]() 为数轴上一动点.
为数轴上一动点.
(1) AB的距离是 .
(2) ①若点![]() 到点
到点![]() 的距离比到点
的距离比到点![]() 的距离大1,点
的距离大1,点![]() 对应的数为 .
对应的数为 .
②若点![]() 其对应的数为
其对应的数为![]() ,数轴上是否存在点
,数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() ,点
,点![]() 的距离之和为8?若存在,请求出
的距离之和为8?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)当点![]() 以每秒钟
以每秒钟![]() 个单位长度从原点
个单位长度从原点![]() 向右运动时,点
向右运动时,点![]() 以每秒钟
以每秒钟![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向左运动,点
向左运动,点![]() 以每秒钟
以每秒钟![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向右运动,问它们同时出发 秒钟时,
向右运动,问它们同时出发 秒钟时,![]() (直接写出答案即可).
(直接写出答案即可).
![]()
参考答案:
【答案】(1)6;(2)①1.5;②-3或5;(3)t=2.
【解析】
(1)根据数轴上任意两点之间的距离等于这两点所表示的数的差的绝对值就可以得出结论;(2)①先表示出PA、PB的值,再根据点![]() 到点
到点![]() 的距离比到点
的距离比到点![]() 的距离大建立方程求出其解即可.
的距离大建立方程求出其解即可.
②①当点P在点A的左侧时,②当点P在点B右侧时,根据题意列方程即可得到结论;
(3)根据行程问题的数量关系和数轴上的点的特征就可以得出结论.
(1)|AB|=|-2-4|=6;
(2) ①设点P表示的数为x,根据题意得,
|x+2|-|4-x|=1,
当x<-2时,方程无解;
当-2≤x<4时,原方程可化为,x+2-4+x=1,解得,x=1.5;
当x≥4时,方程无解.
②若点![]() 在点
在点![]() 的左边,
的左边,![]()
若点![]() 在点
在点![]() 的右边,
的右边,![]()
(3)设t分钟点P到点M,点N的距离相等,
根据题意得,2t+2+t=4-t +3t,
解得:t=2,
答:2分钟点P到点M,点N的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+2x+b的图象可能是( )
A.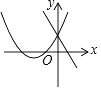
B.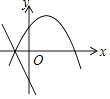
C.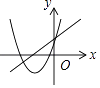
D.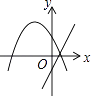
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a﹣b>0,
③a+b+c>0,
④a﹣b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
A.①②③
B.②③④
C.③④⑤
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+2x+b的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a﹣b>0,
③a+b+c>0,
④a﹣b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
A.①②③
B.②③④
C.③④⑤
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在纸面上有一数轴,按要求折叠纸面:
(1)若折叠后数1对应的点与数﹣1对应的点重合,则此时数﹣3对应的点与数 对应的点重合;
(2)若折叠后数2对应的点与数﹣4对应的点重合,则此时数0对应的点与数对 应的点重合;若这样折叠后,数轴上有A、B两点也重合,且A、B两点之间的距离为11(点B在A点的右侧),则点A对应的数为 ,点B对应的数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:
①四边形ABCD是菱形;
②四边形ABCD是中心对称图形;
③四边形ABCD是轴对称图形;
④AC=BD.
其中正确的是(写上正确的序号).
相关试题

