【题目】在平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+2x+b的图象可能是( )
A.
B.
C.
D.
参考答案:
【答案】C
【解析】解:当x=0时,一次函数中y=b,二次函数中y=b,
∴一次函数与二次函数交于点(0,b),
∴B、D不正确;
∵A、C中二次函数图象开口向上,
∴a>0,
∴一次函数y=ax+b为增函数,
∴C选项正确.
故选C.
【考点精析】认真审题,首先需要了解一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远),还要掌握二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某体育用品商店购进一批滑板,每件进价为100元,售价为130元,每星期可卖出80件.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20件.
(1)求商家降价前每星期的销售利润为多少元?
(2)降价后,商家要使每星期的销售利润最大,应将售价定为多少元?最大销售利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+2x+b的图象可能是( )
A.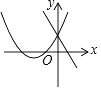
B.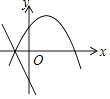
C.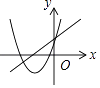
D.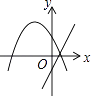
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a﹣b>0,
③a+b+c>0,
④a﹣b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
A.①②③
B.②③④
C.③④⑤
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上点
 对应的数为
对应的数为 ,点
,点 对应的数为
对应的数为 ,点
,点 为数轴上一动点.
为数轴上一动点.(1) AB的距离是 .
(2) ①若点
 到点
到点 的距离比到点
的距离比到点 的距离大1,点
的距离大1,点 对应的数为 .
对应的数为 .②若点
 其对应的数为
其对应的数为 ,数轴上是否存在点
,数轴上是否存在点 ,使点
,使点 到点
到点 ,点
,点 的距离之和为8?若存在,请求出
的距离之和为8?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(3)当点
 以每秒钟
以每秒钟 个单位长度从原点
个单位长度从原点 向右运动时,点
向右运动时,点 以每秒钟
以每秒钟 个单位长度的速度从点
个单位长度的速度从点 向左运动,点
向左运动,点 以每秒钟
以每秒钟 个单位长度的速度从点
个单位长度的速度从点 向右运动,问它们同时出发 秒钟时,
向右运动,问它们同时出发 秒钟时, (直接写出答案即可).
(直接写出答案即可).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c图象对称轴是直线x=1,则下列结论:
①a<0,b<0,
②2a﹣b>0,
③a+b+c>0,
④a﹣b+c<0,
⑤当x>1时,y随x的增大而减小,
其中正确的是( )
A.①②③
B.②③④
C.③④⑤
D.①③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在纸面上有一数轴,按要求折叠纸面:
(1)若折叠后数1对应的点与数﹣1对应的点重合,则此时数﹣3对应的点与数 对应的点重合;
(2)若折叠后数2对应的点与数﹣4对应的点重合,则此时数0对应的点与数对 应的点重合;若这样折叠后,数轴上有A、B两点也重合,且A、B两点之间的距离为11(点B在A点的右侧),则点A对应的数为 ,点B对应的数为 .
相关试题

