【题目】某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
操作发现:
(1)已知,△ABC,如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图 , 并猜想BE与CD的数量关系是 . (要求:尺规作图,不写作法但保留作图痕迹)
类比探究: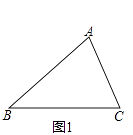
(2)如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么关系?说明理由.
灵活运用: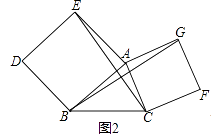
(3)如图3,已知△ABC中,∠ABC=45°,AB=2 ![]() ,BC=3,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.
,BC=3,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.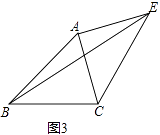
参考答案:
【答案】
(1) ;BE=CD
;BE=CD
(2)
结论:CE=BG且EC⊥BG.
理由:在正方形ABDE和正方形ACFG中,设CE交BG于O,EC交AB于K.
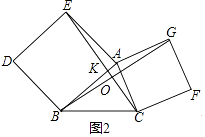
∵AE=AB,AC=AG,∠EAB=∠CAG=90°,
在△ACE和△AGB中,
 ,
,
∴△ACE≌△AGB,
∴CE=BG,∠AEC=∠ABG,
∵∠AKE=∠BKO,
∴∠BOK=∠EAK=90°,
∴EC⊥BG,EC=BG.
(3)
以AB为腰向外作等腰直角三角形Rt△ABG,连接CG.
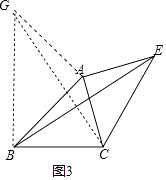
在Rt△ABG中,∵AB=AG=2 ![]()
∴BG= ![]() =4,
=4,
∵∠GBA=∠ABC=45°,
∴∠GBC=90°,
∴CG= ![]() =5,
=5,
∵AG=AB,AE=AC,∠BAG=∠EAC=90°,
∴∠GAC=∠EAB,
在△GAC和△EAB中,
 ,
,
∴△AGC≌△ABE,
∴CG=BE,
∵CG=5,
∴BE=5.
【解析】解:(1)作图如下,
猜想:BE=CD.
理由:∵AB=AD.AC=AE,∠DAB=∠EAC,
∴∠DAC=∠EAB,
在△DAC和△EAB中, ,
,
∴△DAC≌△EAB,
∴CD=BE.
所以答案是BE=CD.
【考点精析】利用等边三角形的性质和正方形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“ ”是规定的这样一种新运算,法则是: ab=a2+2ab .例如 3(2)=32+2×3×(2)=12 .
(1)试求 2(1) 的值;
(2)若 2x=4 ,求 x 的值;
(3)若 (2)x = 2+x ,求 x 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组同学在一周内参加家务劳动时间与人数情况如表所示:
劳动时间(小时)
2
3
4
人数
3
2
1
下列关于“劳动时间”这组数据叙述正确的是( )
A.中位数是2
B.众数是2
C.平均数是3
D.方差是0 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,有点A(0,4)、B(9,4)、C(12,0).已知点P从点A出发沿着AB路线向点B运动,点Q从点C出发沿CO路线向点O运动,运动速度都是每秒2个单位长度,运动时间为t秒.

(1)当t=4.5秒时,判断四边形AQCB的形状,并说明理由.
(2)当四边形AOQB是矩形时,求t的值.
(3)是否存在某一时刻,使四边形PQCB是菱形?若存在,求出t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年,我国政府为减轻农民负担,决定在 5 年内免去农业税.某乡今年人均上缴农业税 25 元,若两年后人均上缴农业税为 16 元,假设这两年降低的百分率相同
(1)求降低的百分率;
(2)小红所在的乡约有 16000 农民,问该乡农民明年减少多少农业税?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)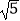 ﹣(
﹣( 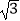 +
+ 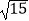 )÷
)÷ 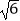 ×
× 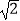
(2)(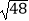 ﹣4
﹣4 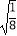 )﹣(3
)﹣(3 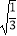 ﹣2
﹣2 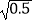 )
)
(3)(3+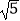 )(3﹣
)(3﹣ 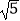 )﹣(
)﹣( 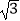 ﹣1)2
﹣1)2
(4)(﹣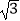 +1)(
+1)( 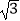 ﹣1)﹣
﹣1)﹣ 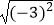 +
+ 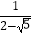 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果xm-3·xn=x2,则n等于( )
A. m-1 B. 5-m C. 4-m D. m+5
相关试题

