【题目】在平面直角坐标系中,有点A(0,4)、B(9,4)、C(12,0).已知点P从点A出发沿着AB路线向点B运动,点Q从点C出发沿CO路线向点O运动,运动速度都是每秒2个单位长度,运动时间为t秒.
(1)当t=4.5秒时,判断四边形AQCB的形状,并说明理由.
(2)当四边形AOQB是矩形时,求t的值.
(3)是否存在某一时刻,使四边形PQCB是菱形?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:结论:四边形AQCB是平行四边形.
理由:∵A(0,4),B(9,4),
∴AB∥OC,AB=9,
当t=4.5秒时,CQ=2t=9,
∴AB=CQ,
∴四边形AQCB是平行四边形.
(2)
解:当四边形AQCB是矩形时,有AB=OQ,
即9=12﹣2t,
∴t=1.5.
∴t=1.5s时,四边形AQCB是矩形.
(3)
解:当PB=CQ时,四边形PQCB是平行四边形,
即9﹣2t=2t,
∴t= ![]() ,
,
此时CQ=2t=4.5,如图作BD⊥OC,垂足为D,
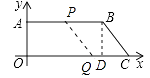
∵B(9,4),C(12,0),
∴BC= ![]() =5,
=5,
∴BC≠CQ,
∴四边形PQCB不是菱形,
即不存在某一时刻,使四边形PQCB是菱形.
【解析】(1)结论:四边形AQCB是平行四边形.只要证明AB=CQ即可解决问题;(2)当四边形AQCB是矩形时,有AB=OQ,即9=12﹣2t,解方程即可解决问题;(3)当PB=CQ时,四边形PQCB是平行四边形,即9﹣2t=2t,可得t= ![]() ,此时CQ=2t=4.5,如图作BD⊥OC,垂足为D,由BC=
,此时CQ=2t=4.5,如图作BD⊥OC,垂足为D,由BC= ![]() =5,推出BC≠CQ,由此即可判断,四边形PQCB不是菱形,即不存在某一时刻,使四边形PQCB是菱形;
=5,推出BC≠CQ,由此即可判断,四边形PQCB不是菱形,即不存在某一时刻,使四边形PQCB是菱形;
【考点精析】掌握平行四边形的判定和菱形的判定方法是解答本题的根本,需要知道两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式3(x2+2xy﹣4y2)﹣(2x2﹣2mxy﹣2y2)中不含xy项,则m= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】“ ”是规定的这样一种新运算,法则是: ab=a2+2ab .例如 3(2)=32+2×3×(2)=12 .
(1)试求 2(1) 的值;
(2)若 2x=4 ,求 x 的值;
(3)若 (2)x = 2+x ,求 x 的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组同学在一周内参加家务劳动时间与人数情况如表所示:
劳动时间(小时)
2
3
4
人数
3
2
1
下列关于“劳动时间”这组数据叙述正确的是( )
A.中位数是2
B.众数是2
C.平均数是3
D.方差是0 -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校活动小组在作三角形的拓展图形,研究其性质时,经历了如下过程:
操作发现:
(1)已知,△ABC,如图1,分别以AB和AC为边向△ABC外侧作等边△ABD和等边△ACE,连接BE、CD,请你完成作图 , 并猜想BE与CD的数量关系是 . (要求:尺规作图,不写作法但保留作图痕迹)
类比探究: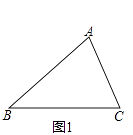
(2)如图2,分别以AB和AC为边向△ABC外侧作正方形ABDE和正方形ACFG,连接CE、BG,则线段CE、BG有什么关系?说明理由.
灵活运用: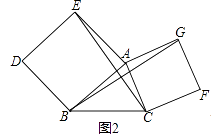
(3)如图3,已知△ABC中,∠ABC=45°,AB=2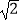 ,BC=3,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.
,BC=3,过点A作EA⊥AC,垂足为A,且满足AC=AE,求BE的长.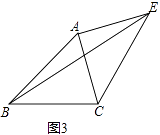
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年,我国政府为减轻农民负担,决定在 5 年内免去农业税.某乡今年人均上缴农业税 25 元,若两年后人均上缴农业税为 16 元,假设这两年降低的百分率相同
(1)求降低的百分率;
(2)小红所在的乡约有 16000 农民,问该乡农民明年减少多少农业税?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)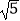 ﹣(
﹣( 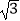 +
+ 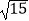 )÷
)÷ 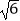 ×
× 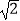
(2)(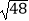 ﹣4
﹣4 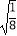 )﹣(3
)﹣(3 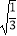 ﹣2
﹣2 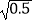 )
)
(3)(3+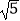 )(3﹣
)(3﹣ 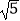 )﹣(
)﹣( 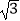 ﹣1)2
﹣1)2
(4)(﹣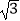 +1)(
+1)( 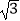 ﹣1)﹣
﹣1)﹣ 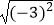 +
+ 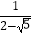 .
.
相关试题

